Kezdőlap


Cím:	A Guldin-féle szabály
Szerző(k):	Lázár Lajos
Füzet:	1901/január, 137 - 139. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A Guldin-féle szabály. Stereometriai feladatok megoldásánál gyakran hivatkozunk a Guldin-féle szabályra, miért is e szabályt s bizonyítását bemutatjuk. E végből kiszámítjuk ama forgási test köbtartalmát, mely az $A B C D$ téglalapnak az $X Y$ tengely körül való forgásából keletkezik.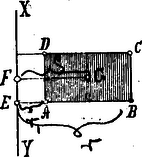

A D = m, E A = r_{1}, E B = r, F G = ρ

, akkor, minthogy

A D

és

B C

hengerfelületet írnak le, a köbtartalom

\begin{matrix} V = (r^{2} - r_{1}^{2}) π m = (r + r_{1}) (r - r_{1}) π m = \end{matrix}

\begin{matrix} = 2 \frac{r + r_{1}}{2} π \cdot A B \cdot m = 2 ρ π t, \end{matrix}

t

a téglalap területe.
Látjuk tehát, hogy a forgási test köbtartalmát megkapjuk, ha a súlypont által leírt utat megszorozzuk a forgó idom területével.
Ha a forgó idom több téglalapból tehető össze, melyeknek területei

t_{1}, t_{2}, t_{3}, t_{4}, ...,

a megfelelő súlypontok távolsága

X Y

-tól pedig

ρ_{1}, ρ_{2}, ρ_{3}, ρ_{4}, ...,

akkor

\begin{matrix} v = 2 ρ_{1} π t_{1} + 2 ρ_{2} π t_{2} + 3 ρ_{3} π t_{3} + ... \end{matrix}

vagy

\begin{matrix} v = 2 π (ρ_{1} t_{1} + ρ_{2} t_{2} + ρ_{3} t_{3} + ...) \end{matrix}

De minthogy a zárójelben levó nyomatékok öszszege

ρ t

, hol

t

az egész idom területe,

ρ

pedig a súlypontjának távolsága

X Y

-tól, azért ismét:

\begin{matrix} v = 2 ρ π t . \end{matrix}

A tétel minden síkidomra alkalmazható, mert minden síkidom tetszésszerinti pontossággal szétbontható csupa apró téglalapra.
E szabály a forgási testek fölületének meghatározására is szolgál.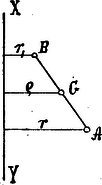

Ha pl.

A B

egyenes forog

X Y

tengely körül, akkor a keletkező kúpfölület területe:

\begin{matrix} F = (r + r_{1}) π \cdot A B = 2 \frac{r + r_{1}}{2} π \cdot A B = 2 ρ π \cdot A B . \end{matrix}

Látjuk tehát, hogy a súlypont útját meg kell szoroznunk a forgó egyenes hosszúságával.
A tétel könnyen bizonyítható akkor is, ha egy tetszésszerinti vonal forog. (L. Holzmüller: Elementar-Mathematik.)
E szabályt már Pappus is ismerte; behatóbban foglalkozott vele Guldin Habakuk Pál (1577-1643) De centro gravitatis czímű munkájában.
E szabályt alkalmazva, könnyen oldhatjuk meg a következő feladatot:

833. Adva van az általános trapéz két párhuzamos oldala

a

és

b

, továbbá a magassága

m

. Meghatározandó a trapéz súlypontjának a távolsága az egyik párhuzamos oldaltól.
Ebben az esetben

\begin{matrix} V = \frac{a + b}{2} m \cdot 2 d π, \end{matrix}

d

a súlypont távolsága

b

-től. De ha a trapéz

b

körül forog

(b > a)

, akkor:

\begin{matrix} V = a m^{2} π + \frac{b - a}{3} m^{2} π - m^{2} π \frac{b + 2 a}{3} \end{matrix}

s így

\begin{matrix} \frac{a + b}{2} m \cdot 2 d π = m^{2} π \frac{b + 2 a}{3}, \end{matrix}

miből

\begin{matrix} d = \frac{m (b + 2 a)}{3 (a + b)} \end{matrix}

(Lázár Lajos, Budapest.)

A feladatot még megoldották: Bayer B., Bogdán G., König D., Lukhaub Gy., Póka Gy., Scharff J., Sasvári J.

sin 18^{\circ}, cos 18^{\circ}

. Megmutatjuk, hogy hogyan számíthatók ki a

cos 18^{\circ}

szög függvényei, a megfelelő szabályos sokszög oldalhosszának ismerete nélkül.

\begin{matrix} cos 18^{\circ} = sin 72^{\circ} = 2 sin 36^{\circ} cos 36^{\circ} \end{matrix}

\begin{matrix} cos 18^{\circ} = 4 sin 18^{\circ} cos 18^{\circ} cos 36^{\circ}, \end{matrix}

tehát

\begin{matrix} 4 sin 18^{\circ} cos 36^{\circ} = 1. \end{matrix}

(1)

Minthogy pedig

\begin{matrix} cos 2 α = 1 - 2 sin^{2} α, \end{matrix}

azért

\begin{matrix} cos 36^{\circ} = 1 - 2 sin^{2} 18^{\circ} \end{matrix}

(2)

legyen most

2 sin 18^{\circ} = x, 2 cos 36^{\circ} = y

, akkor

(1)

és

(2)

-ből:

\begin{matrix} x y = 1 \end{matrix}

\begin{matrix} y + x^{2} = 2, \end{matrix}

mely egyenletekből

\begin{matrix} x^{3} - 2 x + 1 = 0 \end{matrix}

vagy

\begin{matrix} x (x^{2} - 1) - (x - 1) = 0 \end{matrix}

\begin{matrix} (x - 1) [x (x + 1) - 1] = 0, \end{matrix}

miből

\begin{matrix} x^{2} + x - 1 = 0 \end{matrix}

s így

\begin{matrix} x = \frac{\sqrt[]{5} - 1}{2}, y = \frac{1}{x} = \frac{\sqrt[]{5} + 1}{2} . \end{matrix}

Tehát

\begin{matrix} sin 18^{\circ} = \frac{\sqrt[]{5} - 1}{4}, cos 36^{\circ} = \frac{\sqrt[]{5} + 1}{4} . \end{matrix}

\begin{matrix} cos 18^{\circ} = \sqrt[]{\frac{5 + \sqrt[]{5}}{8}}, cos 36^{\circ} = \sqrt[]{\frac{3 - \sqrt[]{5}}{8}} . \end{matrix}