Kezdőlap


Cím:	Coordináta rendszerekről 3.: Coordináta rendszerek a síkban 2.
Szerző(k):	Dr. Horti Henrik
Füzet:	1901/március, 180 - 187. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Coordinata rendszerek a síkban.

C)Sarkcoordináták.

Ha a síkban valamely

O

szilárd pontot választunk, és az

O

pontból úgynevezett

O X

félsugarat húzunk, akkor a sík

R

pontjának a helyzetét tudjuk, ha egyrészt az

R

pontnak

O

ponttól való

ρ

távolságát, másrészt pedig a szöget ismerjük, melyet az

O R = ρ

távolság az

O X

félsugárral alkot. (16. ábra.)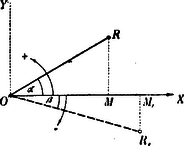

16. ábra

O X

félsugarat sarktengelynek, az

O

pontot sarknak; az

O R = ρ

távolságát radius vectornak és az

α

szöget sarkszögnek nevezzük. A radiusvector és a sarkszög alkotják a pont sarkcoordinátáit.
A radius vectort csak absolut értékében szoktuk számításha venni; a sarkszöget azonban, a sarktengelytől számítva az óramutató járásával ellenkező irányban positívnak, vele megegyező irányban pedig negatívnak vesszük.
(Az ábrában látható

R

pontnak sarkszöge

+

; az

R_{1}

ponté

-

).
Az

R

pont sarkcoordinátáiból könnyű szerrel megtalálhatjuk ugyanannak a pontnak a Cartesius-féle derékszögű coordinátáit és viszont. Ha ugyanis a sarkrendszert olvan derékszögű rendszerrel hozzuk kapcsolatba, melynek kezdőpontját az

O

sarkpontban választjuk és melynek abscissa tengelye a sarktengelyt födi, akkor az

R O M ▵

-ből

\begin{matrix} \frac{R M}{O R} = sin α és \frac{O M}{R M} = cos α; \end{matrix}

vagyis

\begin{matrix} y = ρ sin α és x = ρ cos α, ρ = \pm \sqrt[]{x^{2} + y^{2}} . \end{matrix}

Ezen kapcsolatok alapján szoktuk az egyenleteket transformálni.

D)Homogén coordináták.

Parallel coordinátákra vonatkozó egyenleteken gyakran láthatjuk, hogy ha egyes tagjaiban a bennök előforduló változóknak (ismeretleneknek) hatványkitevőit összeadjuk, az összeg nem minden egyes tagban egyenlő.
Sőt azokban az egyenletekben olyan tagokat (v. tagot) is lelünk, melyek a változókat éppenséggel nem tartalmazzák (más szóval, melyekben a változók az

0

-adik hatványban fordulnak elő.)
Parallel coordinátákban tehát az egyenlet egyes tagjai rendszerint különböző méretűek. Az egyenletek heterogén jellegűek. (Ilyen pl. az

x^{2} + y^{2} - 2 a x + a^{2} - ρ^{2} = 0

; benne az első és a második tag kétméretű, a harmadik egyméretű, a negyedik és az ötödik absolut tagok.)
Homogén coordinátákban az egyenletek más szerkezetűek. Az egyenletek homogének. Homogénnek azt az egyenletet nevezzük, melynek minden egyes tagjában a változók hatványkitevőinek összege egyenlő. Homogén egyenletnek nincsen absolut tagja. Homogén pl.

a x_{1}^{2} + 2 b x_{1} x_{2} + 2 c x_{1} x_{3} + d x_{2}^{2} + 2 e x_{2} x_{3} + f x_{3}^{2} = 0

egyenlet. Benne minden egyes tag kétméretű.
A homogén coordinátáknak ez nagy előnyt biztosít, mert a homogén egyenletek általánosabb jellegű tételek levezetésére alkalmasabbak.
Az a körülmény, hogy bármely nem homogén egyenletet egyszerű transformatiók alapján homogénné lehet tenni, tájékoztatást nyújt egyrészt a parallel és a homogén coordináták közti összefüggésről, másrészt megjelöli az utat, melyen haladnunk kell, ha egyik rendszerről a másikra át akarunk térni. A tudósok kimutatták, hogy a két rendszer között lévő kapcsolat annyira szoros, hogy a parallel coordináták a homogéneknek tulajdonképpen csak specziális esetét képezik.

A homogén coordinátákban is megkülönböztetünk pont- és vonalcoordinátákat.
Homogén pontcoordináták és homogén vonalcoordináták között ugyanaz a különbség, de ugyanaz az összefüggés is van, mint a közönséges pont- és vonalcoordináták között.
A szoros kapcsolat az elemek dualitása.
A rendszerek tényleges bemutatása előtt most mindenek előtt pillantást kellene vetni az eszmék ama egyszerű de szép és érdekes menetére, mely a homogén coordináták fölépítésére vezetett. Mind a mellett mellőzhetem a jelen esetben a részletesebb bevezető magyarázatokat, mert Arany Dániel ugyan e helyen (a III. évf. 3. és 4. számában) "a hely meghatározásról a síkban" cz. a. közölt két czikkében a homogén coordináta rendszerek lényegét ismertette. Midőn tehát ama két czikkre való hivatkozással csak a rendszerek bemutatására szorítkozom, fölhívom a tárgy iránt érdeklődők figvelmét dr. W. Fiedler "Die darstellende Geometrie" czímű jeles munkájának III. kötetére."Die construirende und analytische Geometrie der Lage". E jeles mű a homogén (projectiv) coordináta rendszerek származtatásának egész menetéről minden tekintetben alapos útbaigazítást ad.
1. A pont homogén coordinítái. (Homogén pontcoordináták.)
Ha a síkban valamely

A_{1} A_{2} A_{3}

szilárd coordináta háromszöget választunk, akkor a sík összes pontjait a háromszög három oldalához viszonyíthatjuk. (17. ábra.)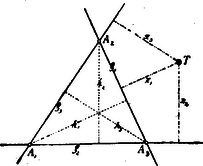

17. ábra

A pont coordinátái alatt ugyanis a pontnak a háromszög oldalaitól mért merőleges távolságait értjük.
Az

A_{2} A_{3}, A_{3} A_{1}

és

A_{1} A_{2}

oldalak a rendszer tengelyei.
Jelöljük a

T

pontnak a tengelyektől való távolságait rendre

x_{1}

-gyel,

x_{2}

-vel és

x_{3}

-mal; akkor

x_{1} x_{2}

és

x_{3}

értékeket a pont trimetrikus (homogén) coordinátáinak nevezzük.
Ha a háromszög oldalait a csúcsokon túl meghosszabbítjuk, a három egyenes (tengely) az egész síkot hét részre osztja. Ha a

T

pont nem pontja a tengelyeknek, akkor bizonyára a hét síkrész egyikében fekszik. Erre való tekintettel nem elegendő, ha a három coordinátának csak absolut értékét ismerjük, hanem a pont teljes meghatározásának czéljából a coordinátákat előjellel látjuk el.
Nevezetesen:
ha a

T

pont és az

A_{1}

csúcs az

A_{2} A_{3}

tengely ugyanazon oldalán van, akkor

x_{1}

positív,
ha a

T

pont és az

A_{2}

csúcs az

A_{3} A_{1}

tengely ugyanazon oldalán van, akkor

x_{2}

positiv,
ha a

T

pont és az

A_{3}

csúcs az

A_{1} A_{2}

tengely ugyanazon oldalán van, akkor

x_{3}

positiv.
Ellenkező esetben a coordináták negativ előjelűek.
(A 17. ábrában

x_{2}

és

x_{3}

positív, ellenben

x_{1}

negatív. Ha a

T

pont a coordináta háromszögön belül feküdnék, akkor mind a három coordinátája positív volna.)
Ha a háromszög oldalait

g_{1}

-gyel,

g_{2}

-vel,

g_{3}

-mal; nemkülönben a háromszög kétszeres területét

▵

-val jelöljük, akkor a coordináták közti összefüggést a

g_{1} x_{1} + g_{2} x_{2} + g_{3} x_{3} = ▵

egyenlet fejezi ki.
(Ennek az egyenletnek a helyességéről könnyű szerrel meggyőződhetünk. Lásd a 17. ábrát.)
Ha az

A_{1} A_{2} A_{3}

háromszög három csúcsának a coordináláit

h_{1}

-gyel,

h_{2}

-vel és

h_{3}

-mal jelöljük, nemkülönben figyelembe vesszük, hogy

g_{1} h_{1} = ▵; g_{2} h_{2} = ▵, g_{3} h_{3} = ▵

vagyis

\begin{matrix} \frac{g_{1}}{▵} = \frac{1}{h_{1}}; \frac{g_{2}}{▵} = \frac{1}{h_{2}}; \frac{g_{3}}{▵} = \frac{1}{h_{3}}, \end{matrix}

ekkor a fönti egyenletet így írhatjuk :

\begin{matrix} \frac{x_{1}}{h_{1}} + \frac{x_{2}}{h_{2}} + \frac{x_{3}}{h_{3}} = 1. \end{matrix}

Ezért bátran mondhatjuk, hogy az

x_{1}, x_{2}

és

x_{3}

számokat csak akkor tekinthetjük a

T

pont homogén coordinatáinak, ha az

\begin{matrix} \frac{x_{1}}{h_{1}} + \frac{x_{2}}{h_{2}} + \frac{x_{3}}{h_{3}} = 1 \end{matrix}

lineáris egyenletnek eleget tesznek.
Az ábra szemléléséből közvetetlenül meggyőződhetünk, hogy a háromszög három csúcsának a coordinátái a következők

\begin{matrix} Az & A_{1} & csúcsé: & x_{1} = h_{1}; & x_{2} = 0; & x_{3} = 0, \\ " & A_{2} & " & x_{1} = 0; & x_{2} = h_{2}; & x_{3} = 0, \\ " & A_{3} & " & x_{1} = 0; & x_{2} = 0; & x_{3} = h_{3}. \end{matrix}

A coordináták értékei szempontjából érdekesek a háromszög úgynevezett "főpontjai". Azok közül a háromszögbe írható (

ρ

sugarú) kör középpontjának coordinátái:

\begin{matrix} x_{1} = ρ_{1}; x_{2} = ρ_{2}; x_{3} = ρ_{3} . \end{matrix}

A háromszög súlypontjának coordinátái :

\begin{matrix} x - 1 = \frac{h_{1}}{3}; x_{2} = \frac{h_{2}}{3}; x_{3} = \frac{h_{3}}{3} . \end{matrix}

\frac{x_{1}}{h_{1}} + \frac{x_{2}}{h_{2}} + \frac{x_{3}}{3} = 1

egyenletet érdekessé teszi az a körülmény, hogy vele az

x_{1}, x_{2}, x_{3}

coordinátákra vonatkozó nem homogén egyenleteket homogénné lehet tenni.

2. Az egyenes vonal homogén coordinítái. (Homogén vonalcoordináták.)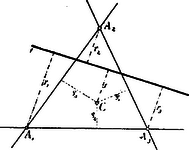

Ha a coordináta-háromszög három csúcsából a

t

egyenesre merőlegest ejtünk, továbbá a síkban tetszés szerint valamely

C

pontot választunk, belőle is a

t

egyenesre merőlegest ejtünk, és ha a csúcspontokból ejtett merőlegeseknek mértékszámait egyenkint a

C

pontból ejtett merőlegesnek mértékszámával elosztjuk, akkor a három hányadost az egyenes vonal három homogén coordinátájának tekinthetjük.

18. ábra

\begin{matrix} Ha az & A_{1} & pont & távolságát & t-től & r_{1}-gyel & jelöljük, \\ " & A_{2} & " & " & " & r_{2}-vel & " \\ " & A_{3} & " & " & " & r_{3}-mal & " \end{matrix}

akkor a

t

egyenes vonal trimetrikus homogén coordinátái:

\begin{matrix} \frac{r_{1}}{r} = u_{1}; \frac{r_{2}}{r} = u_{2}; \frac{r_{3}}{r} = u_{3} . \end{matrix}

Itt is tekintetbe veszszük az előjelet. Nevezetesen:

\begin{matrix} u_{1}-et & positívnak & vesszük & ha & A_{1} & és & C & a & tegyenes & ugyanazon & oldalán & fekszik, \\ u_{2}-t & " & " & " & A_{2} & " & C & " & " & " & " & " \\ u_{3}-t & " & " & " & A_{3} & " & C & " & " & " & " & " \end{matrix}

ellenkező esetben a coordináták negatív előjelűek.
(A 18. ábrában

u_{1}

és

u_{3}

positív;

u_{2}

negatív. Ha a

t

egyenes nem metszi a coordinata háromszöget és a

C

pontot a háromszögön belül választjuk, akkor mind a három coordinata positív.)
Jelöljük a

C

pont coordinátáit (távolságait a háromszög oldalaitól, tehát pontcoordináláit)

ρ_{1}

-gyel,

ρ_{2}

-vel,

ρ_{3}

-mal, akkor a coordináta háromszög három oldalának coordinátái:

\begin{matrix} A_{2} A_{3} & oldalé & u_{1} = \frac{h_{1}}{ρ_{1}}; & u_{2} = 0; & u_{3} = 0; & mert & {\begin{matrix} r_{1} = h_{1} \\ r = ρ_{1} \end{matrix}} \\ A_{3}A_{1} & " & u_{1}=0; & u_{2}=\frac{h_{2}}{ρ_{2}}; & u_{3}=0; & m e r t & {\begin{matrix} r_{2} = h_{2} \\ r = ρ_{2} \end{matrix}} \\ A_{1}A_{2} & " & u_{1}=0; & u_{2}=0; & u_{3}=\frac{h_{3}}{ρ_{3}}; & m e r t & {\begin{matrix} r_{3} = h_{3} \\ r = ρ_{3} \end{matrix}} \end{matrix}

A különböző helyzetű és irányú egyeneseknek a coordinátái rendszerint különböző értékűek.
Azonban, ha két vagy több egyenesnek egy közös coordinátája van, ez annak a jele, hogy az egyeneseknek közös pontjuk van. Ha pl. a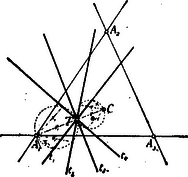

t_{1}, t_{2}, t_{3}, ...

egyenesek coordinátái közül

u_{1}

közös értékű, akkor a

T

pont rajta van az

A_{1}

és

C

pontokat összekötő egyenesen és az

A_{1} C

távolságot az

\frac{A_{1} T}{C T} = \pm u_{1}

viszonyban osztja.
Ha a

T

pont az

A_{1} C

távolságon belül fekszik, akkor a coordináta

-

előjelű (19. ábra).

19. ábra

Ha az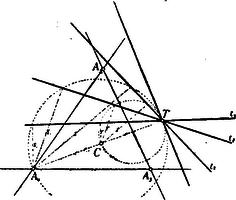

A_{1} C

távolságon kívül esik,

+

előjelű (20. ábra).

20. ábra

Az első esetben az

A_{1}

-ből és a

C

-ből az egyenesekre ejtett merőlegeseknek talppontjai olyan körökön feküsznek, melyek

T

-ben kívülről érintkeznek. A második esetben a körök ‐ a talppontok geometriai helyei ‐ belülről érintkeznek.)
Ha a

t_{1}, t_{2}, t_{3}, ...

egyeneseknek coordinátái közül

u_{2}

közös, akkor

T

metszőpontjuk az

A_{2} C

egyenesen van. A közös coordináta viszonyszáma

\frac{A_{2} T}{C T} = \pm u_{2}

.
Ha végre

u_{3}

közös, akkor a

T

rajta van az

A_{3} C

egyenesen. A viszonyszám

\frac{A_{3} T}{C T} = \pm u_{3}

.
Az esetek bármelyikében a

t_{1}, t_{2}, t_{3}, ...

egyenesek a

T

pontot beburkolják. (Enveloppjai a közös metsző pontjuknak.)
Megjegyezhetjük még, hogy mindazoknak az egyeneseknek, melyek a szilárd

C

ponton áthaladnak, coordinatái:

\begin{matrix} u_{1} = \pm \infty, u_{2} = \pm \infty, u_{3} = \pm \infty . \end{matrix}

Ha a homogén vonalcoordináta-rendszerben is a háromszög kétszeres területét

▵

-val jelöljük, akkor valamely egyenes vonal három homogén coordinátáját a következő egyenlettel kapcsolhatjuk össze:

\begin{matrix} g_{1} ρ_{1} u_{1} + g_{2} ρ_{2} u_{2} + g_{3} ρ_{3} u_{3} = ▵ . \end{matrix}

Tekintettel arra, hogy

g_{1} h_{1} = ▵, g_{2} h_{2} = ▵

, stb. vagyis

\frac{g_{1}}{▵} = \frac{1}{h_{1}}

, stb. az egyenletet így is írhatjuk:

\begin{matrix} \frac{ρ_{1}}{h_{1}} u_{1} + \frac{ρ_{2}}{h_{2}} u_{2} + \frac{ρ_{3}}{h_{3}} u_{3} = 1 \end{matrix}

és mondhatjuk, hogy az

u_{1}, u_{2}, u_{3}

számok csak abban az esetben homogén coordinátái valamely

t

egyenesnek, ha ennek a lineáris egyenletnek eleget tesznek.
Különös jelentőséget nyer ez az egyenlet azzal, hogy vele az

u_{1}, u_{2}, u_{3}

vonalcoordinátákra vonatkoztatott bárminő fokú nem homogén egyenleteket homogénekké lehet átalakítani.

A homogén pont- és vonalcoordinaták kölcsönös összefüggéséről nyújtson némi fogalmat a következők párhuzamba állítása. Azt a föltételt, hogy valamely

T

pont, valamely

t

egyenesen van, vagy megfordítva valamely

t

egyenes valamely

T

ponton áthalad, a következő egyenlet fejezi ki:

\begin{matrix} \frac{1}{h_{1}} u_{1} x_{1} + \frac{1}{h_{2}} u_{2} x_{2} + \frac{1}{h_{3}} u_{3} x_{3} = 0. \end{matrix}

Ennek az egyenletnek kettős jelentősége van. Jelentősége van úgy pontcoordinátákban, mint vonalcoordinátákban.

Ugyanis:

\begin{matrix} Ha benne ategyenes coordinátáit ismerjük, & Ha benne aTpont coordinátáit ismerjük, \\ akkor az egyenletet így írhatjuk: & akkor az egyenletet így írhatjuk: \\ (\frac{u_{1}}{h_{1}}) x_{1} + (\frac{u_{2}}{h_{2}}) x_{2} + (\frac{u_{3}}{h_{3}}) x_{3} = 0, & (\frac{x_{1}}{h_{1}}) u_{1} + (\frac{x_{2}}{h_{2}}) u_{2} + (\frac{x_{3}}{h_{3}}) u_{3} = 0, \\ vagy rövidebben: & vagyis rövidebben: \\ a_{1} x_{1} + a_{2} x_{2} + a_{3} x_{3} = 0. & a_{1} u_{1} + a_{2} u_{2} + a_{3} u_{3} = 0. \\ Ez a homogén vonalas egyenlet homogén & Ez a homogén vonalas egyenlet homogén \\ pontcoordinátákban az egyenes vonalnak az egyenlete. & vonalcoordinátákban az egyenes pontnak az egyenlete. \\ * & * \\ Homogén pontcoordinátákban a másodrendű & Homogén vonalcoordinátákban a másodosztályú \\ görbéknek az egyenlete: & görbéknek az egyenlete: \\ a_{11} x_{1}^{2} + 2 a_{12} x_{1} x_{2} + 2 a_{13} x_{1} x_{2} + a_{22} x_{2}^{2} + & a_{11} u_{1}^{2} + 2 a_{12} u_{1} u_{2} + 2 a_{13} u_{1} u_{3} + a_{22} u_{2}^{2} + \\ + 2 a_{23} x_{2} x_{3} + a_{33} x_{3}^{2} = 0. & + 2 a_{22} u_{2} u_{3} + a_{33} u_{3}^{2} = 0. \end{matrix}