Cím:	Az algebrai függvényekről és az elemi úton megfejthető maximum-minimum feladatokról 5.
Szerző(k):	Dr. Bozóky Endre
Füzet:	1901/január, 133 - 137. oldal	PDF  |  MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. V.   23. Schellbach-féle módszer. Ezt a sok esetben előnyösen alkalmazható módszert Maksay Zsigmond (1850‐1896) ismertette a K. M. L. II. kötetében (34. lap); egyszersmind néhány idevaló feladatot (34., 35., 36., 37. és 54. lap) is közölt. 24. A Steiner-féle feladatra még egyszer, más szempontból, visszatérve, azt vizsgáljuk, vajon két positív változó szorzata, mikor válik maximálissá, ha összegük állandó szám? Már ott azt találtuk, hogy $x+y=2a$ feltétel mellett $xy$ akkor maximális, ha $x=y=a$. Ezt a nevezetes körülményt még egy más úton is igazolhatjuk. Ugyanis, ha $\begin{array}{c}{\displaystyle x+y=2a}\end{array}$ akkor a következő identitás $\begin{array}{c}{\displaystyle 4xy={\left(x+y\right)}^2-{\left(x-y\right)}^2}\end{array}$ ilyen alakot ölt: $\begin{array}{c}{\displaystyle 4xy=4a^2-{\left(x-y\right)}^2}\end{array}$ honnét $\begin{array}{c}{\displaystyle xy=a^2-{\left(\frac{x-y}{2}\right)}^2\mathrm{.}}\end{array}$ E kifejezés akkor maximális értékű, ha a kivonandó eltűnik, tehát ha $x=y$.   25. Közös alap fölött álló, egyenlő kerületű háromszögek közül melyiknek területe a legnagyobb? Ha $a$ az alap, $2s$ a kerület és $b\mathrm{,}c$ a változó oldalak, akkor a terület Heron képlete szerint $\begin{array}{c}{\displaystyle t=\sqrt[]{s\left(s-a\right)\left(s-b\right)\left(s-c\right)}}\end{array}$ $t^2$-nek maximuma ugyanakkor áll elő, a mikor $t$-é; minthogy $\begin{array}{c}{\displaystyle s\left(s-a\right)}\end{array}$ állandó mennyiség, ennélfogva a $\begin{array}{c}{\displaystyle \frac{t^2}{s\left(s-a\right)}=\left(s-b\right)\left(s-c\right)}\end{array}$ kifejezés maximumát kereshetjük. A jobboldali két tényező összege $\begin{array}{c}{\displaystyle s-b+s-c=2s-\left(b+c\right)=a}\end{array}$ állandó mennyiség lévén, tételünk szerint a maximum esete akkor áll be, ha $\begin{array}{c}{\displaystyle s-b=s-c}\end{array}$ vagyis, ha $\begin{array}{c}{\displaystyle b=c\mathrm{.}}\end{array}$   26. Adott gömb köré minimális térfogatú kúp írandó. (K. M. L. 155.) A mellékelt idomot $SA$ mint tengely körül forgatván, egyrészt a gömböt, másrészt a körülírt kúpot kapjuk. Megállapítandó $S$-nek azon helyzete, melyre nézve a kúp minimális köbtartalmú. Hogy maximumról nem lehet szó, azt közvetlenül belátjuk abból, hogy a $G$-től távozó $S$-re nézve a kúp mindinkább közeledik a körülírt hengerhez, ennek térfogata pedig $\infty$. Ha pedig $S$ mindinkább közeledik $G$-hez, akkor a kúp alapköre válik $\infty$-né. Ezen két szélső érték közt kell egy minimumnak feküdnie. Legyen $x$ a kúp magassága, $y$ az alapkör küllője, $R$ a gömb küllője, akkor a kúp köbtartalma $\begin{array}{c}{\displaystyle V=\frac{1}{3}\pi y^{2}x\mathrm{.}}\end{array}$ Ezt a függvényt korábbi közvetlen módszereinkkel bajos volna tárgyalás alá venni. Ily alakban legutóbbi tételünk sem alkalmazható rá közvetlenül. 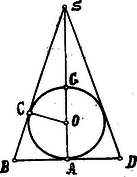    $\begin{array}{c}{\displaystyle BAS▵\sim OCS▵}\end{array}$ miatt $\begin{array}{c}{\displaystyle AB:OC=AS:SC}\end{array}$ vagy $\begin{array}{c}{\displaystyle y:R=x:\sqrt[]{x\left(x-2R\right)}}\end{array}$ honnét $\begin{array}{c}{\displaystyle y^2=\frac{R^{2}x}{x-2R}\mathrm{.}}\end{array}$ Ezt $V$-nek értékénél tekintetbe véve: $\begin{array}{c}{\displaystyle V=\frac{1}{3}\pi R^2\cdot \frac{x^2}{x-2R}\mathrm{.}}\end{array}$ Most már alkalmazhatnók rá a parameteres módszert. Tekintve azt, hogy $V$ kifejezésében csak az $\begin{array}{c}{\displaystyle \frac{x^2}{x-2R}}\end{array}$ tényező változó, következésképpen $V$-nek minimális értéke ezen tényező minimális értékével, vagy a megfordított $\begin{array}{c}{\displaystyle \frac{x-2R}{x^2}}\end{array}$ függvény maximális értékével áll be egyidejűleg. Az utóbbi törtszám $\begin{array}{c}{\displaystyle \frac{1}{x}\left(1-\frac{2R}{x}\right)}\end{array}$ alakban is írható, vagy pedig identikus átalakítással $\begin{array}{c}{\displaystyle \frac{1}{2R}\cdot \frac{2R}{x}\left(1-\frac{2R}{x}\right)}\end{array}$ alakban, s így a térfogat minimális lesz, ha $\begin{array}{c}{\displaystyle \frac{2R}{x}\left(1-\frac{2R}{x}\right)}\end{array}$ maximálissá válik. De ebben a szorzatban a tényezők összege $\begin{array}{c}{\displaystyle \frac{2R}{x}+1-\frac{2R}{x}=1}\end{array}$ s így állandó, s ezért a maximum esetében $\begin{array}{c}{\displaystyle \frac{2R}{x}=1-\frac{2R}{x}}\end{array}$ vagyis $\begin{array}{c}{\displaystyle x=4R}\end{array}$ s így $\begin{array}{c}{\displaystyle y=R\sqrt[]{2}}\end{array}$ s a minimális térfogat $\begin{array}{c}{\displaystyle V=\frac{8}{3}\pi R^3\mathrm{.}}\end{array}$ Ezzel egyidejűleg a következő feladat is megoldást nyert: 27. Adott gömb körül minimális felszínnel bíró kúp írandó. A gömb körül írt idomok térfogatai ezen idomok felszíneivel arányosak lévén, minthogy a minimális térfogatú kúp és a gömb térfogatai úgy aránylanak egymáshoz, mint $2:1$, már előre tudjuk, hogy a minimális felszínű kúpnak kétszer akkora lesz a felszíne, mint az adott gömbé. A kúp felszíne $\begin{array}{c}{\displaystyle F=\pi y\sqrt[]{x^2+y^2}+\pi y^2\mathrm{.}}\end{array}$ A megelőzők szerint $\begin{array}{c}{\displaystyle y:R=x:\sqrt[]{x\left(x-2R\right)}\mathrm{.}}\end{array}$ $\begin{array}{c}{\displaystyle \frac{y}{R}=\frac{\sqrt[]{x^2+y^2}}{x-R}}\end{array}$ honnét $\begin{array}{c}{\displaystyle \sqrt[]{x^2+y^2}=\frac{y\left(x-R\right)}{R}\mathrm{.}}\end{array}$ és $\begin{array}{c}{\displaystyle y^2=\frac{R^{2}x}{x-2R}\mathrm{.}}\end{array}$ Ezeket a felszín kifejezésébe helyettesítvén $\begin{array}{c}{\displaystyle F=\frac{\pi y^2\left(x-R\right)}{R}+\frac{\pi R^{2}x}{x-2R}\mathrm{.}}\end{array}$ A nevezőket eltávolítván $\begin{array}{c}{\displaystyle FR\left(x-2R\right)=\pi y^2\left(x-R\right)\left(x-2R\right)+\pi R^{3}x}\end{array}$ $F$-et paraméternek tekintvén, most alkalmazhatjuk a paraméteres módszert. Előbb azonban tekintetbe véve azt, hogy $\begin{array}{c}{\displaystyle y^2\left(x-2R\right)=R^{2}x}\end{array}$ felírhatjuk azt, hogy $\begin{array}{c}{\displaystyle FR\left(x-2R\right)=\pi R^{2}x\left(x-R\right)+\pi R^{3}x}\end{array}$ s a lehetséges összevonások után: $\begin{array}{c}{\displaystyle \pi R^{2}x-Fx+2RF=0}\end{array}$ $x$ reálitásának föltétele: $\begin{array}{c}{\displaystyle F^2-8\pi R^{2}F\geqq 0}\end{array}$ más szóval $\begin{array}{c}{\displaystyle F\geqq 8\pi R^2\mathrm{.}}\end{array}$ A minimum esete beáll, ha $\begin{array}{c}{\displaystyle F=8\pi R^2;}\end{array}$ de akkor $\begin{array}{c}{\displaystyle x=\frac{F}{2\pi R}=4R}\end{array}$ mint a megelőző feladatban. Az eddigiek begyakorlására oldjuk meg a következő feladatokat: 893. $\left(a\right)$ Egy $R$ küllőjű körben az átmérőre merőleges húrt húzván, ennek végpontjait összekötjük az átmérő végpontjaival. Mily föltétel mellett lesz a húr, mint közös alap fölött álló két háromszög területeinek különbsége maximális? $\left(b\right)$ Egy állandó kerületű téglalap oldalaira mint átmérőkre a téglalapon kívül fekvő félköröket rajzolunk. Mikor válik az így keletkezett idom területe minimálissá? $\left(c\right)$ Az $a$ oldalú szabályos háromszögbe minimális területű szabályos háromszög írandó. $\left(d\right)$ Egy $R$ sugarú félkör átmérőjén fölveszünk egy pontot. Az így keletkezett szeletek mint átmérők fölött félköröket rajzolunk. Állapítsuk meg annak föltételét, hogy a keletkezett holdacs területe maximálissá váljék, és vizsgáljuk meg, miként változik ez a terület, ha a fölvett pont az átmérőn végig halad? 894. $\left(e\right)$ Egy $R$ sugarú körben húzzuk meg azt a húrt, mely a körnek a húrral párhuzamos átmérője körül való forgatása közben maximális felületű hengerpalástot ír le. 895. $\left(f\right)$ Egy adott szám úgy bontandó két részre, hogy azon összeg, melynek egyik tagja az első és második rész hányadosa, másik tagja pedig ezen hányados reciprok értéke, minimálissá váljék. $\left(g\right)$ Egy adott szám úgy bontandó két részre, hogy a részek négyzetgyökeinek összege maximális legyen.