Kezdőlap


Cím:	Az algebrai függvényekről és az elemi úton megfejthető maximum-minimum feladatokról 2.
Szerző(k):	Dr. Bozóky Endre
Füzet:	1900/október, 36 - 42. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

6. A függvény értékének változása. Függvényünk egyértékű lévén, a független változó minden értékéhez a függő változónak egy és csakis egy értéke tartozik. E két összetartozó számérték a függvény egy értékrendszere. Másrészt a függvény folytonos lévén, az egyik értékrendszerről a másikra való átmenetel közben megszakítás sehol sincs. Ha tehát a derékszögű coordinaták segítségével a függvénynek egymásra következő értékrendszereit, mint a síknak pontjait ábrázoljuk, akkor a független változó értékeit, mint abscissákat, a hozzájuk tartozó függő változó értékeket, mint ordinatákat tekintjük, s megszerkesztjük a függvényhez tartozó görbe vonalat.

7. A

2

-od fokú algebrai egész függvény ábrázolása. Föltételezzük azt, hogy az

\begin{matrix} y = a x^{2} + b x + c \end{matrix}

függvénynek

a

együtthatója positív. Tárgyalásunk most már az

\begin{matrix} a x^{2} + b x + c = 0 \end{matrix}

vegyes másodfokú egyenlet gyökeinek természete szerint

3

eshetőséggel áll szemben.
I. Az egyenletnek gyökei

x'

és

x''

valósak, s egymástól külömbözőek. Ennek föltétele az, hogy a discriminans:

b^{2} - 4 a c > 0

, vagyis positív.
Az egyenlet többtagúját a gyöktényezőkkel fejezzük ki:

\begin{matrix} y = a x^{2} + b x + c = a (x - x') (x - x'') . \end{matrix}

(1)

Másrészt az ismeretes átalakítások után :

\begin{matrix} y = a [{(x + \frac{b}{2 a})}^{2} - \frac{b^{2} - 4 a c}{4 a^{2}}] . \end{matrix}

(2)

közvetlenül világos, hogy

x = - \infty

esetében (2) alapján

y = + \infty

.
Minthogy a discriminans föltétel szerint positív, ennélfogva (2)-ben a kivonandó szintén positív szám. Addig, míg

x

- \infty

-től kiindulva a negatív számsor mentén növekszik, a kisebbítendőnek értéke is növekszik.

\begin{matrix} x = 0 esetében y = c . \end{matrix}

Addig míg

x

a positív számsor mentén növekszik, (2)-ben a kisebbítendő mindinkább nagyobbodván,

y

-nak értéke is növekedőleg halad, s

x = + \infty

esetében ismét

y = + \infty

lesz.
Az eddigiek még nem myújtanak tiszta képet. De tekintsük most az

x', x "

gyököket. Tudjuk, hogy

\begin{matrix} x = x' esetében y = 0 \end{matrix}

\begin{matrix} x = x'' esetében y = 0 \end{matrix}

tehát a függvény értéke kétszer veszi föl a zérus értéket. Föltéve, hogy

x'' < x'

, akkor a

- \infty

-től kezdődőleg növekedő független változó mellett a függvény értéke először

x = x''

esetében, másodszor

x = x'

esetében válik zérussá. Ha a függvény folytonos, akkor ezen két érték között negatívvá kell válnia, még pedig oly módon, hogy

x''

-től kezdve értéke fogy, majd

x

-nek egy bizonyos értékétől kezdve ismét növekszik, hogy másodszor átmehessen a

O

-on. Lássunk egy példát.

\begin{matrix} y = x^{2} - 8 x + 12 \end{matrix}

a megelőzők szerint így írható föl:

\begin{matrix} = a [{(x - \frac{8}{2})}^{2} - \frac{64 - 4 \cdot 12}{4}] \end{matrix}

\begin{matrix} y = {(x - 4)}^{2} - 4. \end{matrix}

A függvény értékváltozásait az

x

-nek

x = - \infty

-től

x = + \infty

-ig való változása közben csak a legjellemzőbb esetekre vonatkozólag számítván, a következő táblázatot állíthatjuk össze :

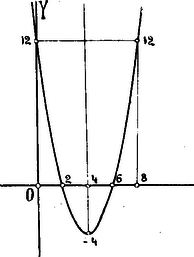
\begin{matrix} \begin{matrix} x & -\infty & 0 & 2 & 4 & 6 & 8 & +\infty \\ y & +\infty & 12 & 0 & -4 & 0 & 12 & +\infty \end{matrix} \end{matrix}

A függvényt ábrázoló görbét ebből a

7

pontból megrajzolhatjuk.

A rajznak kettős előnye van :

1.

megtekintése a függvény változásáról tisztább képet nyújt mint a milyent akármilyen, még oly részletességgel kidolgozott értékrendszer- táblázat nyújthatna; 2. a görbe vonalban a parabolára ismerünk.
Az

x = 4, y = - 4

értékrendszer a parabola tetőpontját adja meg. A függvény az

x = 2 ... 6

intervallum mentén negatív értéket vesz fel. Az

x = - \infty ... 4

intervallumban a függvény értéke fogy, az

x = 4 ... + \infty

intervallumban pedig ismét növekedik. A fogyás és növekedés közös határa a parabola tetőpontja; itt veszi föl a függvény a lehető legkisebb értéket. Mikor a függvény fogyásból növekedésbe megy át, akkor azt mondjuk róla, hogy minimumát éri.
Visszatérve az általános eset tárgyalására, kérdés,

x

-nek mely értékére nézve veszi föl

y

e minimális értéket? A (2) alaknak puszta megtekintéséből láthatjuk, hogy a külömbség alakjában kifejezett

y

értéke akkor válik minimálissá, ha a kisebbítendője

\begin{matrix} {(x + \frac{b}{2 a})}^{2} = 0, \end{matrix}

tehát ha

\begin{matrix} x = - \frac{b}{2 a} . \end{matrix}

Ennék az értéknek megfelelőleg

\begin{matrix} y = - \frac{b^{2} - 4 a c}{4 a} . \end{matrix}

II. Az egyenletnek gyökei valósak és egymás közt egyenlők. Ennek föltétele az, hogy

\begin{matrix} b^{2} - 4 a c = 0. \end{matrix}

Ebben az esetben

\begin{matrix} y = a {(x + \frac{b}{2 a})}^{2} \end{matrix}

alakot ölti, s a függvénynek egyáltalában nincsenek negatív értékei. A minimum esete ismét

\begin{matrix} x = - \frac{b}{2 a} \end{matrix}

mellett áll be, melyhez az

y = 0

érték tartozik. Például legyen

\begin{matrix} y = 9 x^{2} - 6 x + 1 \end{matrix}

akkor

\begin{matrix} y = {(3 x - 1)}^{2} \end{matrix}

alakban állítható elő. A legjellemzőbb értékrendszerek táblázata most:

\begin{matrix} \begin{matrix} x & -\infty & 0 & \frac{1}{3} & \frac{2}{3} & +\infty \\ y & +\infty & 1 & 0 & 1 & +\infty \end{matrix} \end{matrix}

III. Az egyenletnek gyökei képzetesek. Ennek föltétele az, hogy

b^{2} - 4 a c < 0

, vagyis a discriminans negatív.
Az

\begin{matrix} y = a [{(x - \frac{b}{2 a})}^{2} - \frac{b^{2} - 4 a c}{4 a^{2}}] \end{matrix}

alak most azt mutatja, hogy a függvény a független változónak minden értékére nézve positív értéket vesz föl. A minimum akkor áll be, ha ez az első tag eltűnik, tehát

\begin{matrix} x = - \frac{b}{2 a} . \end{matrix}

Például:

\begin{matrix} y = 4 x^{2} - 5 x + 3, \end{matrix}

miből

\begin{matrix} y = 4 {(x - \frac{5}{8})}^{2} + \frac{23}{16} . \end{matrix}

8. Ha a negatív. Ebben az esetben a független változónak az abscissa tengely mentén való növekedése közben a függő változó ugyanazon az értéksorozaton halad át, mint a melyen positív

a

esetében, csakhogy mindvégig ellenkező előjellel.

Ha tehát

x

- \infty

-től

- \frac{b}{2 a}

-ig növekszik, e közben

y

- \infty

-től

\frac{4 a c - b^{2}}{4 a}

-ig növekszik;

x

-nek

- \frac{b}{2 a}

-tól

+ \infty

-ig növekedése közben pedig

y

\frac{4 a c - b^{2}}{4 a}

-tól

- \infty

-ig csökkenik. A függvény az

x = - \frac{b}{2 a}

értékre nézve maximumát éri.
Az

a x^{2} + b x + c = 0

egyenlet gyökeinek természete szerint ismét

3

eset lehetséges, a szerint, a mint a két gyök valós; (pl.

y = - x^{2} + 4 x - 3)

; a gyökök egyenlőek (pl.

y = - x^{2} + 4 x - 4)

és a gyökök képzetesek (pl.

y = - x^{2} + 6 x - 17

9. Végeredmények. A megelőzőket egybevetve, a következő tételt nyerjük:
Az

y = a x^{2} + b x + c

függvény a közben, míg a független változó

- \infty

-től

+ \infty

-ig halad, positív

a

esetében

+ \infty

-től kezdve a minimális

\frac{4 a c - b^{2}}{4 a}

értékig csökkenőleg, innét kezdve

+ \infty

-ig növekedőleg halad; negatív

a

esetében

- \infty

-től maximális

\frac{4 a c - b^{2}}{4 a}

értékig növekedőleg, innét kezdve

- \infty

-ig csökkenőleg halad.
Ha a függvény maximális vagy minimális értékeit, (melyek csakis külön-külön léphetnek föl) egy szóval eminens-értékeknek nevezzük, akkor a föntebbi tételt még így is kifejezhetjük:
Az

y = a x^{2} + b x + c

függvény a független változónak

- \frac{b}{2 a}

értéke esetében eminens értéküvé válik, és pedig maximumát, illetőleg minimumát éri, a szerint, amint az a együttható negatív, illetőleg positív.
A függvénnyel kapcsolatos parabola tengelye az abscissák tengelyére merőleges lévén, az eminens értéknek megfelelő tetőpontjában érintője az abscissák tengelyével párhuzamos.
Annak eldöntése, vajon az eminens érték maximum-e avagy minimum, attól függ, hogy a görbe vonal a kérdéses pont közelében homorú-e avagy domború-e az abscissa tengelyre nézve? Ezek után lássunk nehány példát!

10. Osszunk föl egy adott a hosszúságot oly két részre, hogy a részek fölött alakított egyenlő oldalú háromszögek területeinek összege minimális legyen.
Nevezzük

a

-nak egyik részét

x

-nek; akkor a másik rész

(a - x)

. Az ezen oldalak fölött szerkesztett egyenlő oldalú háromszögek területeinek összege

\begin{matrix} y = \frac{1}{4} x^{2} \sqrt[]{3} + \frac{1}{4} {(a - x)}^{2} \sqrt[]{3} \end{matrix}

\begin{matrix} y = \frac{\sqrt[]{3}}{2} (x^{2} - a x + \frac{a^{2}}{2}) . \end{matrix}

E függvény minimuma beáll, ha

\begin{matrix} x = \frac{a}{2} \end{matrix}

értéke pedig

\begin{matrix} y = \frac{\sqrt[]{3}}{8} \cdot a^{2} . \end{matrix}

11. Keressük meg

x

-nek, azt az értékét, a mely mellett az

\begin{matrix} y = {(a_{1} - x)}^{2} + {(a_{2} - x)}^{2} + ... + {(a_{n} - x)}^{2} \end{matrix}

függvény minimális értéket vesz föl.

\begin{matrix} y = n x^{2} - 2 \sum a \cdot x + \sum a^{2} . \end{matrix}

Minthogy

x^{2}

-nek együtthatója positív, tehát az eminens érték tényleg minimum, s beáll, ha

\begin{matrix} x = \frac{1}{n} \sum a . \end{matrix}

Ha tehát valamely ismeretlen

x

számnak az értékét

n

számú astronomiai, physikai, geod

ℵ

tikai vagy más megfigyeléssel akarjuk meghatározni, és az igazi

x

szám helyett az észlelés hibáival pontatlanított

a_{1} a_{2} ... a_{n}

eredményekhez jutunk, akkor az egyes mérésekből nyert számok arithmetikai középarányosa adja meg az

x

-nek legvalószinűbb értékét, föltéve, hogy valamennyi mérés vagy megfigyelés egyformán megbízható. A kérdéses esetben ugyanis a legkisebb négyzetösszegek módszere szerint az

\begin{matrix} (a_{1} - x), (a_{2} - x), ... (a_{n} - x) \end{matrix}

hibák négyzeteinek összege minimummá válik.

12. Az adott

a

alap fölött szerkesztett

2 s

kerületű háromszögek közül melyiknek területe a legnagyobb?

x

a keresett háromszögnek második oldala, akkor a harmadik oldal (

2 s - a - x

) s így területe a Heron-féle képlet szerint :

\begin{matrix} y = \sqrt[]{s (s - a) (s - x) (a + x - s)} \end{matrix}

honnét:

\begin{matrix} y^{2} = s (s - a) [- x^{2} + (2 s - a) x - s (s - a)] . \end{matrix}

A függvény értékének négyzete tehát maximális értékűvé válik, ha

\begin{matrix} x = s - \frac{a}{2} \end{matrix}

honnét

\begin{matrix} 2 s - a - x = s - \frac{a}{2} \end{matrix}

vagyis a keresett háromszög egyenlő szárú és területe

\begin{matrix} y = \frac{a}{2} \sqrt[]{s (s - a)} . \end{matrix}