Kezdőlap


Feladat:	5464. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Seprődi Barnabás Bendegúz
Füzet:	2023/május, 304 - 305. oldal		PDF \| MathML
Témakör(ök):	Feladat, Egyenletesen változó mozgás (Változó mozgás), Egyenesvonalú mozgás lejtőn
Hivatkozás(ok):	Feladatok: 2023/február: 5464. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Használjuk ki a parabola azon tulajdonságát, hogy bármely pontja egyenlő távol van az $F$ fókuszponttól és a $v$ vezéregyenestől.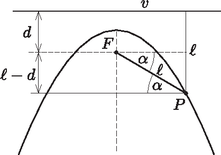
Legyen $F$ és $v$ távolsága $d$ , a lejtő hajlásszöge $α$ , a pálya hossza ( $F$ és $P$ távolsága) pedig $ℓ$ . Ekkor

\begin{matrix} ℓ sin α = ℓ - d, vagyis ℓ = \frac{d}{1 - sin α} . \end{matrix}

Csúszás közben a pontszerű test egyenletesen gyorsul, a gyorsulása (súrlódásmentes esetben)

a = g sin α

, így a csúszás

t

idejére fennáll:

\begin{matrix} \frac{g sin α}{2} t^{2} = ℓ = \frac{d}{1 - sin α}, \end{matrix}

vagyis

\begin{matrix} t = \sqrt[]{\frac{2 d}{g}} \cdot \frac{1}{\sqrt[]{sin α (1 - sin α)}} . \end{matrix}

A csúszás ideje akkor lesz minimális, ha az

\begin{matrix} f (α) = sin α (1 - sin α) \end{matrix}

kifejezés maximális. A fenti kifejezés a

ξ \equiv sin α

változónak kvadratikus függvénye:

\begin{matrix} f (ξ) = ξ (1 - ξ), \end{matrix}

ami a legnagyobb értékét

ξ = \frac{1}{2}

-nél, vagyis

α = 30^{\circ}

-nál éri el. (Ezt teljes négyzetté alakítással, vagy deriválással láthatjuk be.)

Megjegyzés. Érdekes, hogy a legrövidebb lecsúszási időhöz tartozó

α

szög sem a parabola

d

paraméterétől, sem a nehézségi gyorsulástól nem függ. Ezt a részletes számítás elvégzése nélkül, dimenzionális megfontolásokkal (dimenzióanalízissel) is beláthatjuk. A dimenziótlan

α

szög csak a méter mértékegységű

d

-től és a

{m/s}^{2}

mértékegységű

g

-től függhetne. Mivel az idő mértékegysége csak

g

-ben szerepel,

α

nem függhet

g

-től. Ekkor viszont

α

d

-től sem függhet, hiszen nincs egy másik, hosszúság dimenziójú mennyiség, ami

d

mértékegységét kiejthetné.