Feladat: 2004. évi Kürschák matematikaverseny 1. feladata Korcsoport: 18- Nehézségi fok: nehéz
Füzet: 2005/február, 67 - 69. oldal  PDF  |  MathML 
Témakör(ök): Matematika, Kürschák József (korábban Eötvös Loránd), Síkgeometriai bizonyítások, Körülírt kör, Hozzáírt körök
Hivatkozás(ok):Feladatok: 2005/február: 2004. évi Kürschák matematikaverseny 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Alkalmazzunk inverziót az A-val szemközti hozzáírt körre, melynek középpontját F jelöli. Az ABC háromszög oldalai (mivel érintik e kört) mind azonos sugarú körökbe transzformálódnak. Feltehetjük, hogy ez a sugár egységnyi, és a megfelelő körök középpontjai OA,OB és OC. Az ABC körülírt körének a képe az A', B' és C' pontokon átmenő k1 kör lesz. (A vesszős változat az adott pont inverzió utáni képet jelöli.)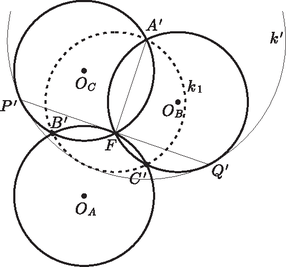
Azt állítjuk, hogy a k1 kör szintén egyégnyi sugarú. OA, OB és OC ugyanis egyaránt egységnyi távolságra vannak az F-től, így a rajtuk átmenő kör sugara is egységnyi. Az OAOBOC háromszög oldalfelezőpontjai által meghatározott háromszög körülírt körének sugara tehát 12. E háromszög csúcsai az FA', FB' és FC' szakaszok felezőpontjai, tehát az említett 12 sugarú kört egy F közepű 2-szeres nagyítás a k1-be viszi, mely így csakugyan egységsugarú.

 
 

Az A' körüli 2 egység sugarú kör belülről érinti az AB, ill. AC oldalak képeit és a körülírt kör képét is, így e kör éppen k képe lesz az inverzió során. A P', Q' pontok pedig az A'-vel átellenes pontok a megfelelő egyégsugarú körökön, ezért A'FP' és A'FQ' egyaránt derékszögek, továbbá F (a szimmetria miatt) felezi P'Q'-t. Mivel F volt az inverzió középpontja, F egyúttal a PQ szakaszt is felezi.  □
 
Megjegyzések. 1. Hasonlóan a tavalyi verseny első feladatához, idén sem volt haszontalan a síkbeli inverzió tulajdonságainak ismerete (jóllehet tavaly többen próbálkoztak az alkalmazásával). A versenybizottság fenntartja magának az inverzióval (is) megoldható példa kitűzésének jogát.
2. A feladat szoros rokonságot mutat az 1978. évi Nemzetközi Matematikai Diákolimpián kitűzött 4. feladattal. A különbség lényegében annyi, hogy az olimpiai feladatban a k kör belülről érintett, és az érintési pontok alkotta szakasz felezőpontja a beírt kör középpontja volt. Az említett feladatra megjelent1 egyik szellemes megoldás ötlete könnyen alkalmazható a mi esetünkre is. Ezt vázoljuk az alábbiakban.
3. Több versenyző próbálkozott az analitikus módszerrel. Természetesen így is teljes értékű megoldás kapható, azonban viszonylag kevesen jártak sikerrel.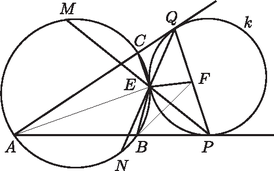
 
II. megoldás. Legyen E a k kör és az ABC háromszög körülírt körének érintési pontja, M, ill. N pedig a PE, ill. QE egyeneseknek és a háromszög körülírt körének E-től különböző metszéspontja. Mivel E-ből a k kört egy középpontos hasonlóság viszi az ABC háromszög körülírt körébe, az M-ben, ill. N-ben a körülírt körhöz húzott érintők párhuzamosak AB-vel, ill. AC-vel. Eszerint M felezi a C-t tartalmazó AB ívet, N pedig felezi a B-t tartalmazó AC ívet.
 
 

Felhasználva a kerületi szögek egyenlőségét, illetve hogy feleakkora ívhez feleakkora kerületi szög tartozik
MEB∢=MEA∢+AEB∢=β+α2+γ=π+γ2
adódik, ahonnan
BEP∢=π-MEB∢=α+β2.
(Felhasználtuk, hogy α+β+γ=π.)
Világos, hogy ABEC húrnégyszög, így a konkáv BEC∢ nagysága π+α. Legyen F az iménti szög felezőjének és a PQ szakasznak a metszéspontja. Eszerint
BEF∢=π+α2,ésAPF∢=π-α2,
hiszen az AQP háromszög egyenlő szárú. Azt kaptuk, hogy FEBP húrnégyszög, melyben a PF íven nyugvó kerületi szögre
PBF∢=PEF∢=BEF∢-BEP∢=π+α2-α+β2=π-β2.
Az adódott tehát, hogy BF az ABC háromszög B-nél lévő külső szögének a felezője.
A fenti számolás értelemszerű módosításával adódik, hogy CF az ABC háromszög C-nél levő külső szögfelezője. A két külső szögfelező F metszéspontja egyfelől a BC oldalhoz hozzáírt kör középpontja, másfelől rajta van az ABC háromszög A-ból induló szögfelezőjén. E szögfelező azonban felezi az egyenlő szárú APQ háromszög alapját, az állítást igazoltuk.  □
1ld. Reiman ‐ Dobos: Nemzetközi Matematikai Diákolimpiák 1959‐2003 (328‐332. oldal)