Feladat:	2022. évi Nemzetközi Matematika Diákolimpia 21. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Molnár-Szabó Vilmos
Füzet:	2022/november, 450 - 451. oldal		PDF  |  MathML
Témakör(ök):	Matematika, Nemzetközi Matematikai Diákolimpia, Síkgeometriai bizonyítások, Húrnégyszögek, Egyéb sokszögek geometriája
Hivatkozás(ok):	Feladatok: 2022/szeptember: 2022. évi Nemzetközi Matematika Diákolimpia 21. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.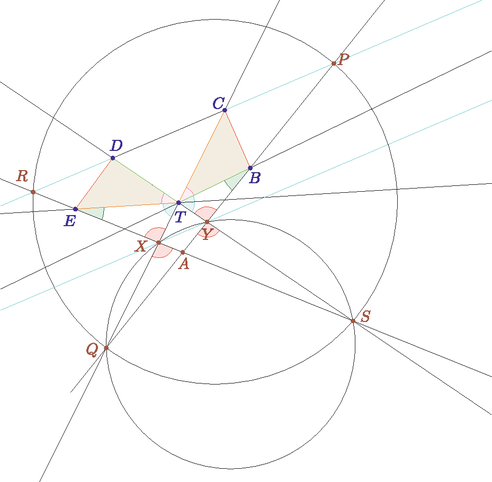     A szakaszhosszok egyenlőségeiből következik, hogy $TBC▵\cong TDE▵$. Legyen az $AE$ és $TQ$ egyenesek metszéspontja $X$, az $AB$ és $DT$ egyeneseké pedig $Y$. Egy kis szögszámolással megmutatjuk, hogy $EXT▵\sim BYT▵$. Az egybevágó háromszögekből $ETD\sphericalangle =CTB\sphericalangle$, továbbá $DTX\sphericalangle =CTY\sphericalangle$ (csúcsszögek), tehát $ETX\sphericalangle =DTX\sphericalangle -ETD\sphericalangle =CTY\sphericalangle -CTB\sphericalangle =BTY\sphericalangle$. Tudjuk még, hogy $ABT\sphericalangle =TEA\sphericalangle$, tehát valóban egymáshoz hasonlóak az $EXT$ és $BYT$ háromszögek. Emiatt az is igaz, hogy $EXT\sphericalangle =BYT\sphericalangle$, amiből pedig következik, hogy $QXS\sphericalangle =EXT\sphericalangle =BYT\sphericalangle =QYS\sphericalangle$. Mivel $QAX\sphericalangle =SAY\sphericalangle$ is teljesül, így az $XQA$ és $YSA$ háromszögek hasonlóak, és ezért $CQP\sphericalangle =XQY\sphericalangle =XSY\sphericalangle =RSD\sphericalangle$. Az $EXT$ és $BYT$ háromszögek hasonlóságából következik továbbá, hogy $\frac{TX}{TE}=\frac{TY}{TB}$. Mivel $TE=TC$ és $TB=TD$, ebből $\frac{TX}{TC}=\frac{TY}{TD}$, ami azt jelenti, hogy $XYCD$ trapéz. A hasonló háromszögek egymásnak megfelelő $XTE\sphericalangle$ és $BTY\sphericalangle$ szögeinek egyenlőségéből $BTQ\sphericalangle =STE\sphericalangle$. Mivel a feltétel szerint $ABT\sphericalangle =AET\sphericalangle$, a $TQB$ és $TSE$ háromszögek is hasonlóak, hiszen megfelelő szögeik egyenlőek. A hasonlóság miatt $\begin{array}{c}{\displaystyle QT:ST=TB:TE\mathrm{,}\text{így}QT\cdot TC=QT\cdot TE=ST\cdot TB=ST\cdot TD\mathrm{,}}\end{array}$ azaz a $Q$, $S$, $C$, $D$ pontok egy körön vannak. Emiatt a $QCP$ háromszög külső szögeként $QCR\sphericalangle =QPR\sphericalangle +CQP\sphericalangle$, azaz $QPR\sphericalangle =QCR\sphericalangle -CQP\sphericalangle$. Mivel $QSCD$ húrnégyszög, $QSD\sphericalangle =QCD\sphericalangle$. Végül $\begin{array}{c}{\displaystyle QPR\sphericalangle =QCR\sphericalangle -CQP\sphericalangle =QSD\sphericalangle -RSD\sphericalangle =QSR\sphericalangle \mathrm{,}}\end{array}$ tehát $SQPR$ húrnégyszög.