Feladat:	5415. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Somlán Gellért
Füzet:	2022/november, 505 - 506. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Áramvezetőre ható erő, Faraday-féle indukciótörvény, Áram hőhatása (Joule-hő)
Hivatkozás(ok):	Feladatok: 2022/május: 5415. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Megoldás. Az ellenállás nélküli huzal és a fémrúd zárt áramkört alkot, amelyben a változó mágneses fluxus miatt feszültség indukálódik, áram folyik és hő fejlődik. $a)$ A $0\le t\le t_0$ időintervallumban az indukált feszültséget a nyugalmi indukció összefüggése alapján számíthatjuk. Mivel a mágneses indukció nagysága $\Delta t=t_0$ idő alatt (egyenletesen változva) nulláról $B_0$-ra nő, a hurok területe pedig $L^2/2$, Faraday törvénye szerint az indukált feszültség $\begin{array}{c}{\displaystyle U=\frac{\Delta \Phi }{\Delta t}=\frac{\Delta B}{\Delta t}\cdot \frac{L^2}{2}=\frac{B_0{L}^2}{2t_0}\mathrm{.}}\end{array}$ Ekkora feszültség az $R=Lr$ ellenállású áramkörben $\begin{array}{c}{\displaystyle I_a=\frac{U}{R}=\frac{B_{0}L}{2r{t}_0}}\end{array}$ erősségű áramot hoz létre, és így $t_0$ idő alatt $\begin{array}{c}{\displaystyle Q_a=I_a^{2}R{t}_0=\frac{B_0^2{L}^3}{4r{t}_0}}\end{array}$ hő fejlődik. $b)$ A $t_0\le t\le 3t_0$ időintervallumban a mágneses indukció nagysága állandó $B_0$, viszont a fémrúdnak a vezetékek közé eső részének $\ell$ hossza egyre nagyobb lesz: $\begin{array}{c}{\displaystyle \ell \left(t\right)=L+v_0\left(t-t_0\right)\mathrm{.}}\end{array}$ Az áramkörben indukálódott feszültség a mozgási indukció törvénye szerint $\begin{array}{c}{\displaystyle U\left(t\right)=B_0{v}_0\ell \left(t\right)\mathrm{,}}\end{array}$ tehát időben változik, de az áramkör ellenállása is ugyanilyen ütemben növekszik: $R\left(t\right)=r\ell \left(t\right)$. A kialakuló áramerősség: $\begin{array}{c}{\displaystyle I_b=\frac{U\left(t\right)}{R\left(t\right)}=\frac{B_0{v}_0\ell \left(t\right)}{r\ell \left(t\right)}=\frac{B_0{v}_0}{r}=\text{állandó}\mathrm{.}}\end{array}$ Ez az áramerősség akkor egyezik meg a korábban kiszámított $I_a$ áramerősséggel, ha $\begin{array}{c}{\displaystyle \frac{B_0{v}_0}{r}=\frac{B_{0}L}{2r{t}_0}\mathrm{,}}\end{array}$ vagyis a rúd sebessége $\begin{array}{c}{\displaystyle v_0=\frac{L}{2t_0}\mathrm{.}}\end{array}$ A rúd vezetékek közötti részének hossza a mozgás végén $\begin{array}{c}{\displaystyle \ell \left(3t_0\right)=2t_0{v}_0=2L\mathrm{.}}\end{array}$ $c)$ Amikor a rúd még nem mozog, a feszültség is és az áramerősség is állandó, tehát a hőfejlődés teljesítménye is időben állandó $P_0$. A rúd mozgása során az áramerősség időben állandó, de a rúdnak az áramvezetésben részt vevő hossza $L$-ről $2L$-re nő, és emiatt az ellenállása is a kezdeti érték kétszerese lesz. Ennek megfelelően a teljesítmény is időben (egyenletesen) változik, és a mozgás végén $2P_0$ lesz. Ábrázoljuk a hőfejlődés teljesítményét az idő függvényében. A grafikon alatti területek a fejlődött hő nagyságát adják meg. 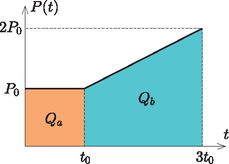    Az ábráról leolvasható, hogy $\begin{array}{c}{\displaystyle Q_a=P_0{t}_0\mathrm{,}\text{illetve}{Q}_b=\frac{P_0+2P_0}{2}\cdot 2t_0=3P_0{t}_0\mathrm{,}}\end{array}$ vagyis $Q_b=3Q_a$.