Kezdőlap


Feladat:	5414. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Somlán Gellért
Füzet:	2022/november, 503 - 504. oldal		PDF \| MathML
Témakör(ök):	Vezető ellenállásának számítása, Feladat, Egyéb ellenállás-kapcsolások
Hivatkozás(ok):	Feladatok: 2022/május: 5414. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.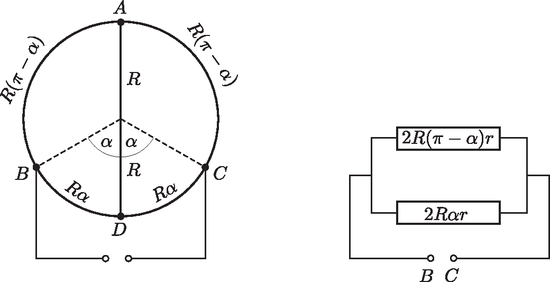

Megoldás. Legyen a huzal egységnyi hosszúságú darabjának ellenállása

r

. Határozzuk meg először a

B

és a

C

pontok közötti eredő ellenállást. Mivel az egyenes vezeték végpontjai (az elrendezés szimmetriája miatt) ekvipotenciálisak, közöttük nem folyik áram, az átmérő menti vezeték tehát eltávolítható (1. ábra).

1. ábra

\begin{matrix} R_{B C} = {(\frac{1}{2 R (π - α) r} + \frac{1}{2 R α r})}^{- 1} = 2 R r \frac{α (π - α)}{π} . \end{matrix}

A

és

B

pontok közötti eredő ellenállást a 2. ábra alapján lépésről lépésre számolhatjuk.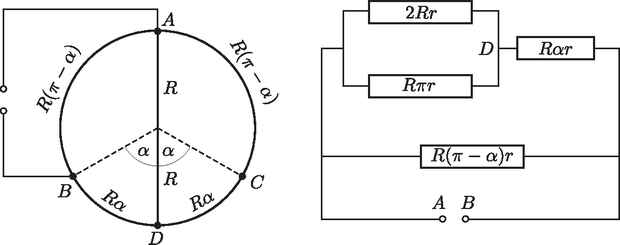

2. ábra

A felső ág bal oldalán látható párhuzamosan kapcsolt ellenállások eredője:

\begin{matrix} R_{1} = \frac{2 R r \cdot R π r}{2 R r + R π r} = \frac{2 R π}{2 + π} r . \end{matrix}

A felső ág két sorosan kapcsolt ellenállásának eredője:

\begin{matrix} R_{2} = R_{1} + R α r = \frac{2 π + π α + 2 α}{π + 2} R r, \end{matrix}

végül pedig (algebrai átalakítások után)

\begin{matrix} R_{A B} = \frac{(π - α) R r \cdot R_{2}}{(π - α) R r + R_{2}} = \frac{(π - α) (2 π + 2 α + π α)}{π (π + 4)} R r . \end{matrix}

R_{A B} = R_{B C}

feltétel szerint fennáll, hogy

\begin{matrix} 2 R r \frac{α (π - α)}{π} = \frac{(π - α) (2 π + 2 α + π α)}{π (π + 4)} R r . \end{matrix}

Ennek az egyenletnek az egyik megoldása:

α_{1} = π

. Ha ez teljesül, akkor az

A

B

és

C

pontok egybeesnek, és így nyilván

R_{A B} = R_{B C} = 0

. Számunkra ez a gyök érdektelen, hiszen ebben az esetben nem is beszélhetünk

A B

és

A C

ívekről. Az egyenlet másik gyöke:

\begin{matrix} α_{2} = \frac{2 π}{6 + π} \approx 0, 69 radián, \end{matrix}

és így a keresett ívhosszak:

\begin{matrix} \overset{⏜}{A B} = \overset{⏜}{B C} = (π - α_{2}) R = π \frac{4 + π}{6 + π} R \approx 2, 45 R . \end{matrix}