Kezdőlap


Feladat:	5410. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Téglás Panna
Füzet:	2022/november, 500 - 501. oldal		PDF \| MathML
Témakör(ök):	Feladat, Egyenletes mozgás (Egyenes vonalú mozgások)
Hivatkozás(ok):	Feladatok: 2022/május: 5410. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az ábra alapján az emelkedés és a siklás teljes idejére érvényes: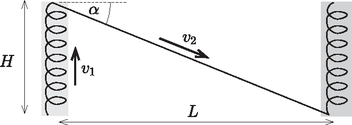

\begin{matrix} t = \frac{H}{v_{1}} + \frac{L}{v_{2} cos α} . \end{matrix}

Mivel

\begin{matrix} cos α = \frac{L}{\sqrt[]{H^{2} + L^{2}}} és v_{2} = k sin α = k \frac{H}{\sqrt[]{H^{2} + L^{2}}}, \end{matrix}

az egyik termik aljától a következő termik aljáig

\begin{matrix} t = \frac{H}{v_{1}} + \frac{L^{2} + H^{2}}{k H} \end{matrix}

(1)

idő alatt jut el a vándorsólyom.
Ha valahonnan ismernénk

t

értékét, akkor annak segítségével az (1) egyenletből ki tudnánk számítani az emelkedés

H

magasságát. Rendezés után egy (

H

-ra nézve) másodfokú egyenlethez jutunk:

\begin{matrix} (k + v_{1}) H^{2} - k v_{1} t H + v_{1} L^{2} = 0. \end{matrix}

Ennek csak akkor van (valós) megoldása, ha a diszkrimináns nem negatív:

\begin{matrix} k^{2} v_{1}^{2} t^{2} - 4 (k + v_{1}) v_{1} L^{2} \geq 0, \end{matrix}

vagyis

\begin{matrix} t \geq \frac{2 L}{k} \sqrt[]{\frac{k + v_{1}}{v_{1}}} = t_{min} . \end{matrix}

b)

Ezek szerint egy-egy repülési ciklus legrövidebb ideje a fenti

t_{min}

, ami a megadott számadatok mellett kb. 980 s, azaz 16,3 perc.

a)

A legrövidebb időhöz tartozó emelkedési magasság:

\begin{matrix} H = \frac{v_{1} k t_{min}}{2 (k + v_{1})} = L \sqrt[]{\frac{v_{1}}{k + v_{1}}} \approx 816 m . \end{matrix}

c)

A fentebb kiszámolt optimális ,,menetidőhöz'' tartozó siklási szög:

\begin{matrix} α = arctg \sqrt[]{\frac{v_{1}}{k + v_{1}}} \approx 22^{\circ} . \end{matrix}