Feladat:	5400. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Seprődi Barnabás Bendegúz
Füzet:	2022/november, 495 - 496. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Tehetetlenségi erők, Egyenletes körmozgás
Hivatkozás(ok):	Feladatok: 2022/április: 5400. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Megoldás. Célszerű a bolygóhoz rögzített, forgó koordináta-rendszerből szemlélni a helyzetet. Ebben a rendszerben a gravitációs gyorsulás (${\text{<span style="font-weight: bold;"><span style="font-style: italic;">g</span></span>}}_{\text{grav}}$) mellett fellép egy $r{\omega }^2$ nagyságú, a bolygó forgástengelyére merőleges, attól ,,elfele'' mutató centrifugális gyorsulás (${\text{<span style="font-weight: bold;"><span style="font-style: italic;">g</span></span>}}_{\text{cf}}$), ahol $r$ a forgástengelytől mért távolság, $\omega$ pedig a bolygó szögsebessége. A gravitációs gyorsulás $g_0$ nagysága csak a bolygó középpontjától mért távolságtól függ, tehát a bolygó felszínén mindenhol ugyanakkora. Az eredő nehézségi gyorsulás a gravitációs és a centrifugális gyorsulás vektori összege (lásd az ábrát):   $\begin{array}{c}{\displaystyle \text{<span style="font-weight: bold;"><span style="font-style: italic;">g</span></span>}={\text{<span style="font-weight: bold;"><span style="font-style: italic;">g</span></span>}}_{\text{grav}}+{\text{<span style="font-weight: bold;"><span style="font-style: italic;">g</span></span>}}_{\text{cf}}\mathrm{.}}\end{array}$   Feltételezzük,hogya fák$$g-velellentétesiránybannőnek. Tudjuk,hogyaz $R$sugarúbolygóegyenlítője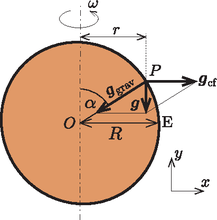(E)mentén   $\begin{array}{c}{\displaystyle |{\text{<span style="font-weight: bold;"><span style="font-style: italic;">g</span></span>}}_{\text{cf}}|=R{\omega }^2\text{és}|\text{<span style="font-weight: bold;"><span style="font-style: italic;">g</span></span>}|=\mathrm{0,}}\end{array}$   tehátfennáll,hogy$$ g_0$=R$ {\omega }^2$$.     Tekintsünk most egy tetszőleges $P$ pontot a bolygó felszínén, és legyen az $OP$ egyenesnek a forgástengellyel bezárt szöge $\alpha$. Az ábrán jelölt koordináta-rendszerben a gyorsulások komponensei:   ${\displaystyle \begin{array}{cccc}\hfill {\displaystyle g_{\text{grav}\mathrm{,}x}}& {\displaystyle =-g_0\text{sin}\alpha \mathrm{,}}\hfill & {\displaystyle g_{\text{grav}\mathrm{,}y}}\hfill & \hfill {\displaystyle =-g_0\text{cos}\alpha \mathrm{,}}\\ \hfill {\displaystyle g_{\text{cf}\mathrm{,}x}}& {\displaystyle =r{\omega }^2=R{\omega }^2\text{sin}\alpha \mathrm{,}}\hfill & {\displaystyle g_{\text{cf}\mathrm{,}y}}\hfill & \hfill {\displaystyle =\mathrm{0,}}\end{array}}$ és így $\begin{array}{c}{\displaystyle g_x=g_{\text{grav}\mathrm{,}x}+g_{\text{cf}\mathrm{,}x}=-g_0\text{sin}\alpha +R{\omega }^2\text{sin}\alpha =\text{sin}\alpha \left(R{\omega }^2-g_0\right)=\mathrm{0,}}\end{array}$   valamint$$ g_y$=-$ g_0$$cos$\alpha$. Ezekszerinta fákezena furcsabolygóna forgástengellyelpárhuzamosannőnek,mivela centrifugálisgyorsulásellensúlyozzaa gravitációsgyorsulásnaka forgástengelyremerőlegeskomponensét.Az északiféltekéntehát,,felfelé'',a délin,,lefelé''fognaknőnia fák.   Seprődi Barnabás Bendegúz (Budapest, Óbudai Árpád Gimn., 10. évf.)   Megjegyzés. Az egyenlítőn, ahol súlytalanság van, feltehetően egyáltalán nem nőnek fák, vagy ha mégis, akkor azok irányát nem a nehézségi erő, hanem valami más (pl. a fény) határozhatná meg.