Kezdőlap


Feladat:	B.5173	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bán-Szabó Áron , Baski Bence , Bencsik Ádám , Bencsik Dávid , Bognár András Károly , Diaconescu Tashi (Románia) , Duchon Márton , Fekete Richárd , Hegedűs Dániel , Kalocsai Zoltán , Kercsó-Molnár Anita , Koleszár Domonkos , Kovács Tamás , Kökényesi Márk Péter , Mohay Lili Veronika , Molnár-Szabó Vilmos , Móricz Benjámin , Nádor Benedek , Páhán Anita Dalma , Romaniuc Albert-Julian , Seres-Szabó Márton , Simon László Bence , Somogyi Dalma , Terjék András József , Varga Boldizsár , Wiener Anna , Zömbik Barnabás
Füzet:	2022/április, 218 - 220. oldal		PDF \| MathML
Témakör(ök):	Matematika, Feladat, Síkgeometriai bizonyítások, Forgatva nyújtás, Középponti és kerületi szögek
Hivatkozás(ok):	Feladatok: 2021/április: B.5173

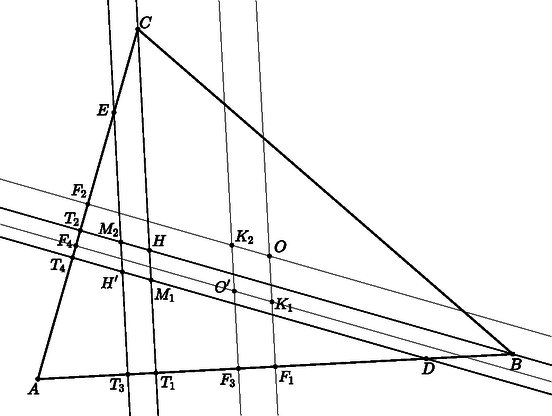
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük az $A B C ▵$ -ben az $A B$ , illetve $A C$ oldalakhoz tartozó magasságvonalak talppontját $T_{1}$ -gyel és $T_{2}$ -vel, az $A D E ▵$ -ben az $A D$ és $A E$ oldalakhoz tartozó magasságvonalak talppontját pedig $T_{3}$ -mal és $T_{4}$ -gyel. Legyen $T_{1} H \cap T_{4} H' = M_{1}$ és $T_{2} H \cap T_{3} H' = M_{2}$ , az $A B$ , illetve $A C$ szakaszok felezőpontja $F_{1}$ és $F_{2}$ , az $A D$ , illetve $A E$ szakaszok felezőpontja $F_{3}$ és $F_{4}$ , továbbá $F_{1} O \cap F_{4} O' = K_{1}$ és $F_{2} O \cap F_{3} O' = K_{2}$ .

Vegyük észre, hogy az

O

és

O'

pontok nem eshetnek egybe, mert például

D

belső pontja az

A B C

háromszög köréírt körének, így

O D < O A

, míg

O' D = O' A

. Ezért az

O O'

szakasz nem fajulhat egy ponttá. Mivel

E A D ∢ = C A B ∢

hegyesszög, az

A B C

és az

A D E

háromszög magasságpontja sem lehet az

A

pont, tehát

H \neq A

és

H' \neq A

.
Tekintsük most a

H' M_{1} H M_{2}

és az

O' K_{1} O K_{2}

négyszögeket, amelyeknek szemközti oldalaik mind merőlegesek

A B

-re, illetve

A C

-re, ezért mindkét négyszög paralelogramma. Az egyik paralelogramma megfelelő oldalai páronként párhuzamosak a másik paralelogramma megfelelő oldalaival, hiszen mind az oldalfelező merőlegesek, mind a magasságvonalak merőlegesek a megadott oldalra, továbbá a megfelelő csúcsoknál (

H' \leftrightarrow O'

H \leftrightarrow O

) ugyanakkora belső szögek vannak, hiszen mindkettőt két

A

-hoz közelebbi egyenes (

T_{3} H'

T_{4} H'

, illetve

F_{3} O'

és

F_{4} O'

) határolja, amelyek párhuzamosak. Ebből következően a

H' M_{1} H

és az

O' K_{1} O

háromszögek azonos körüljárási irányúak, valamint két-két oldaluk páronként párhuzamos (

H' M_{1} ∥ O' K_{1}

és

H M_{1} ∥ O K_{1})

, így ha

H H' ∥ O O'

, akkor a szóban forgó háromszögek hasonlók, tehát megfelelő oldalaik hosszának aránya megegyezik:

\begin{matrix} \frac{H' M_{1}}{H M_{1}} = \frac{O' K_{1}}{O K_{1}} . \end{matrix}

Ez tehát szükséges feltétele annak, hogy

H H' ∥ O O' .

Ez a feltétel azonban elégséges is, mert ha teljesül, akkor a

H' M_{1} H

és

O' K_{1} O

háromszögek hasonlók, azaz a harmadik oldalpár is párhuzamos. Kimondhatjuk tehát, hogy

H H' ∥ O O'

akkor és csakis akkor teljesül, ha

\begin{matrix} \frac{H' M_{1}}{H M_{1}} = \frac{O' K_{1}}{O K_{1}} . \end{matrix}

(1)

Most vizsgáljuk meg a

H' M_{1} H M_{2}

paralelogramma oldalainak arányát. Ismert, hogy egy paralelogramma területét kiszámíthatjuk egy oldal hosszának és az oldalhoz tartozó magasság hosszának szorzataként:

\begin{matrix} T_{H' M_{1} H M_{2}} = H M_{1} \cdot T_{1} T_{3} = H' M_{1} \cdot T_{2} T_{4}, \end{matrix}

amiből azt kapjuk, hogy

\begin{matrix} \frac{H M_{1}}{H' M_{1}} = \frac{T_{2} T_{4}}{T_{1} T_{3}}, \end{matrix}

ahol a nevezők értéke nem

0

, hiszen a feladat feltételei szerint

E

A C

szakasz belső pontja, ezért

E H'

nem eshet egybe

C M_{1}

-gyel. Mivel

A B T_{2} ∢

és

A C T_{1} ∢

, merőleges szárú hegyesszögek, ezért egyenlő nagyságúak, így egy megfelelő egybevágósági transzformációval fedésbe hozhatók egymással. Ekkor alkalmazhatjuk a párhuzamos szelőszakaszok tételét a következőképpen:

\begin{matrix} \frac{T_{2} T_{4}}{T_{1} T_{3}} = \frac{B D}{C E}, \end{matrix}

ami a fentiek értelmében azt jelenti, hogy

\begin{matrix} \frac{H M_{1}}{H' M_{1}} = \frac{T_{2} T_{4}}{T_{1} T_{3}} = \frac{B D}{C E}, tehát \frac{B D}{C E} = \frac{H M_{1}}{H' M_{1}} . \end{matrix}

O' K_{1} O K_{2}

paralelogramma esetében az előzőekhez hasonlóan azt kapjuk, hogy

\begin{matrix} \frac{O K_{1}}{O' K_{1}} = \frac{F_{2} F_{4}}{F_{1} F_{3}} . \end{matrix}

Számoljuk ki az

F_{2} F_{4}

és

F_{1} F_{3}

szakaszok hosszát. Mivel

F_{2}

A C

szakasz felezőpontja, ezért

A F_{2} = \frac{A C}{2}

, az

F_{4}

pedig az

A E

szakasz felezőpontja, így

\begin{matrix} A F_{4} = \frac{A E}{2} = \frac{A C - C E}{2} = A F_{2} - \frac{C E}{2}, \end{matrix}

amiből

\begin{matrix} F_{2} F_{4} = \frac{C E}{2} \end{matrix}

következik. Hasonlóképpen

F_{1} F_{3} = \frac{B D}{2}

, így

\begin{matrix} \frac{O K_{1}}{O' K_{1}} = \frac{F_{2} F_{4}}{F_{1} F_{3}} = \frac{\frac{C E}{2}}{\frac{B D}{2}} = \frac{C E}{B D} . \end{matrix}

Beláttuk tehát, hogy

\frac{H M_{1}}{H' M_{1}} = \frac{B D}{C E}

és

\frac{O K_{1}}{O' K_{1}} = \frac{C E}{B D}

, amit

(1)

-gyel összevetve azt kapjuk, hogy

\begin{matrix} \frac{B D}{C E} = \frac{C E}{B D}, \end{matrix}

s mivel szakaszok hosszai pozitív számok, ebből

\begin{matrix} B D = C E \end{matrix}

következik. Ez tehát szükséges feltétel, már csak azt kell megmutatnunk, hogy elégséges is. Mivel az előbbiekben csupa egyenlőséggel dolgoztunk, ezek megfordítva is igazak, így a bizonyítás végére értünk.

Koleszár Domonkos (Miskolc, Herman Ottó Gimn., 11. évf.),

Kökényesi Márk Péter (Budapest, Szent István Gimn., 11. évf.),

Varga Boldizsár (Verőce, Géza Fejedelem Református Ált. Isk., 8. évf.)