Kezdőlap


Feladat:	5364. fizika feladat	Korcsoport: -	Nehézségi fok: -
Megoldó(k):	Dóra Márton
Füzet:	2022/április, 243 - 244. oldal		PDF \| MathML
Témakör(ök):	Feladat, Pontrendszerek mozgásegyenletei
Hivatkozás(ok):	Feladatok: 2021/december: 5364. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. A kis testre a nehézségi erő hat lefelé, valamint a félhenger által kifejtett nyomóerő a félhenger felszínére merőlegesen. A félhengerre a gravitációs erő hat lefelé, az alátámasztás által kifejtett nyomóerő fölfelé, és a kis testre kifejtett nyomóerő ellenereje. Vízszintes irányban külső erő nem hat, a rendszer vízszintes irányú lendülete állandó, végig nulla, mint a kezdeti pillanatban. Ez úgy lehetséges, ha a henger sebessége és a kis test sebességének vízszintes komponense azonos nagyságú és ellenkező irányú (1. ábra).
Az energiamegmaradás törvénye szerint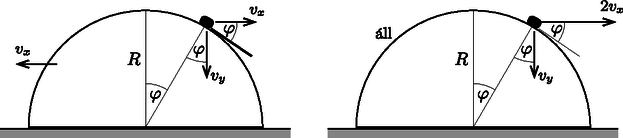

\begin{matrix} m g R = m g R cos φ + \frac{1}{2} m v_{x}^{2} + \frac{1}{2} m (v_{x}^{2} + v_{y}^{2}), \end{matrix}

\begin{matrix} 1. ábra \end{matrix}

\begin{matrix} 2. ábra \end{matrix}

[htb

ahonnan

\begin{matrix} 2 g R (1 - cos φ) = 2 v_{x}^{2} + v_{y}^{2} . \end{matrix}

(1)

A félhengerrel együtt mozgó vonatkoztatási rendszerben a félhenger áll, a kis test pedig egy kör mentén, a kör érintőjének irányában mozog. A kis test sebességének vízszintes komponense

2 v_{x}

. Kényszerfeltétel, hogy a körpálya érintőjére merőleges sebességkomponens nulla:

v_{y} cos φ = 2 v_{x} sin φ

. Ezt (1)-be helyettesítve kapjuk, hogy

\begin{matrix} v_{x}^{2} = g R \frac{1 - cos φ}{1 + 2 tg^{2} φ} . \end{matrix}

Amíg a kis test a félhenger felszínén mozog, addig

v_{x}

nem csökkenhet, hiszen a kör felszínére merőleges kényszererő vízszintes komponense a félhenger sebességével azonos irányba mutat, a nehézségi erőnek és a talaj nyomóerejének pedig nincs vízszintes komponense. A kis test akkor válik el a kör felszínéről, amikor a félhenger által kifejtett kényszererő nullává válik, vagyis amikor

v_{x}

értéke a legnagyobb. Ez ott következik be, ahol az

\begin{matrix} f (φ) = \frac{1 - cos φ}{1 + 2 tg^{2} φ} \end{matrix}

függvénynek maximuma van a

[0; π / 2]

intervallumon. Szélsőértékszámítással, vagy

f (φ)

grafikus ábrázolásával belátható, hogy

φ = φ_{max} \approx 0, 75 (rad) \approx 43^{\circ}

szögnél van a maximum, így a kis testnek a félhenger felszínén megtett útja:

\begin{matrix} s = R φ_{max} \approx 0, 75 R . \end{matrix}

Dóra Márton (Budapest, ELTE Apáczai Csere J. Gyak. Gimn., 12. évf.)