Kezdőlap


Feladat:	5356. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Gábriel Tamás , Seprődi Barnabás Bendegúz
Füzet:	2022/február, 119 - 121. oldal		PDF \| MathML
Témakör(ök):	Feladat, Hajítások
Hivatkozás(ok):	Feladatok: 2021/november: 5356. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A szöcske az elugrása után parabolapályán fog mozogni. Ez a parabola nyilván a gerenda leghosszabb oldalélére merőleges síkban fekszik, elegendő tehát ezt a síkot vizsgálni. (Ha a szöcskének lenne ,,hosszanti'' irányú sebessége, akkor ennek nullára csökkentésével csökkenthetné az energiaráfordítást.)
Ha a szöcske pályagörbéje a gerenda felső éleitől véges távolságra haladna, akkor az elugrás helyének és irányának változatlanul tartása mellett kisebb kezdősebesség (kisebb energiaráfordítás) is elegendő lenne (1. ábra). A szaggatott vonallal jelölt parabolapályánál kedvezőbb a folytonos vonallal jelölt pályához tartozó mozgás. A pályagörbének tehát legalább az egyik felső élet ,,érintenie'' kell, annak közvetlen közelében kell elhaladnia. Ha ugyanekkor nem érintené a gerenda másik felső élét, akkor (a kezdősebességet és az elugrás szögét változatlannak tartva) az elugrás helyének megváltoztatásával olyan parabolához juthatnánk, amelyik a gerenda felett, attól véges távolságban halad, tehát ez sem lehet a legkedvezőbb elrendezés (2. ábra).

\begin{matrix} 1. ábra \end{matrix}

\begin{matrix} 2. ábra \end{matrix}

[htb
Optimális esetben a parabola szimmetriatengelye a gerenda téglalap alakú keresztmetszetének függőleges középvonalánál található, és a parabola illeszkedik a téglalap mindkét felső csúcsára. A 3. ábra jelöléseit használva felírhatjuk, hogy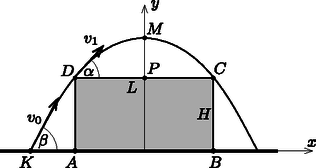

\begin{matrix} v_{1} t cos α = \frac{L}{2}, valamint v_{1} sin α = g t, \end{matrix}

ahol

t

azt az időt jelöli, amennyi alatt a szöcske a

D

pontból a pályagörbe legmagasabb (

M

-mel jelölt) pontjába kerül. Ebből a két egyenletből

t

kiküszöbölése után kapjuk, hogy

\begin{matrix} v_{1}^{2} = \frac{g L}{sin (2 α)} . \end{matrix}

3. ábra

Írjuk fel most az energiamegmaradás törvényét a

K

és

D

pontok közötti mozgásra:

\begin{matrix} \frac{1}{2} m v_{0}^{2} = \frac{1}{2} m v_{1}^{2} + m g H, \end{matrix}

vagyis

\begin{matrix} v_{0}^{2} = 2 g H + v_{1}^{2} = 2 g H + \frac{g L}{sin (2 α)} . \end{matrix}

Innen leolvashatjuk, hogy

v_{0}

akkor minimális (akkor legkisebb a szöcske energiaráfordítása az elugráskor), amikor

sin (2 α) = 1

, vagyis

α = 45^{\circ}

.
Határozzuk meg a parabola

\begin{matrix} f (x) = a x^{2} + b x + c \end{matrix}

alakban keresett egyenletét a 3. ábrán látható koordináta-rendszerben. Mivel a

C = (\frac{L}{2}, H)

és a

D = (- \frac{L}{2}, H)

pontok rajta vannak a parabolán, teljesül, hogy

\begin{matrix} H = a {(\frac{L}{2})}^{2} + b \frac{L}{2} + c, illetve H = a {(- \frac{L}{2})}^{2} - b \frac{L}{2} + c . \end{matrix}

Ezekből következik, hogy

b = 0

és

c = H - a \frac{L^{2}}{4}

, vagyis a parabola egyenlete:

\begin{matrix} f (x) = a (x^{2} - \frac{L^{2}}{4}) + H . \end{matrix}

Láttuk, hogy a parabola meredeksége a

D

pontban

tg α = tg 45^{\circ} = 1

. A parabola ismert tulajdonsága szerint ez a meredekség éppen kétszerese a

D M

szelő meredekségének:

\begin{matrix} 1 = 2 \frac{- a L^{2} / 4}{L / 2}, ahonnan a = - \frac{1}{L}, \end{matrix}

tehát a pályagörbe egyenlete:

\begin{matrix} f (x) = H + \frac{L}{4} - \frac{x^{2}}{L} . \end{matrix}

Megjegyzés. Ugyanezt az összefüggést differenciálszámítással is megkaphatjuk.

f' (x) = 2 a x

, ami az

x_{D} = - L / 2

helyen

- 2 a L / 2 = 1

, vagyis

a = - 1 / L

A szöcske elugrásának

x_{K} < 0

koordinátáját az

f (x_{K}) = 0

feltételből kapjuk meg:

\begin{matrix} x_{K} = - \sqrt[]{H L + \frac{L^{2}}{4}}, \end{matrix}

vagyis az elugrási hely és a gerenda szélének

K A

távolsága

\begin{matrix} d = \sqrt[]{H L + \frac{L^{2}}{4}} - \frac{L}{2} . \end{matrix}

Az elugrás szögét a vízszintes irányú sebesség állandóságát kifejező

v_{0} cos β = v_{1} cos 45^{\circ}

összefüggésből kaphatjuk meg:

\begin{matrix} cos β = \frac{v_{1}}{\sqrt[]{2} v_{0}} = \sqrt[]{\frac{L}{2 (L + 2 H)}}, \end{matrix}

amit így is kifejezhetünk:

\begin{matrix} tg β = \sqrt[]{1 + \frac{4 H}{L}} . \end{matrix}

Megjegyzés. Ezt az összefüggést differenciálszámítással is megkaphatjuk. Az

f (x)

függvény deriváltja az

x_{K} = - \sqrt[]{H L + (L^{2} / 4)}

helyen:

\begin{matrix} tg β = f' (x_{K}) = - 2 a x_{K} = \sqrt[]{1 + \frac{4 H}{L}} . \end{matrix}

Hátra van még a legkisebb energiaráfordításhoz tartozó parabolapálya fókuszpontjának meghatározása. A szimmetria miatt ez a pont a gerenda

M P

szimmetriatengelyén, vagyis az

y

tengelyen található. Egy optikai analógia segítségével könnyen beláthatjuk, hogy a fókuszpont éppen a

D C

szakasz felezőpontja, vagyis a gerenda felső lapjának

P

pontja. Képzeljük el, hogy a szöcske pályagörbéje egy parabolatükörnek (forgásparaboloidnak) a szimmetriatengelyére illeszkedő síkkal való metszete. Ha erre a tükörre az

A D

egyenes mentén haladó fénysugár esik, az (

α = 45^{\circ}

miatt) vízszintesen halad tovább. Másrészt a tükör szimmetriatengelyével párhuzamos fénysugarak a fókuszpont irányába verődnek vissza, a fókuszpont tehát csakis a

P

pont lehet. (Ennél a megfontolásnál hallgatólagosan felhasználtuk azt a tényt is, hogy a parabola geometriai értelemben vett fókuszpontja és a parabolatükör fizikai értelemben vett fókuszpontja egybeesik.)

Gábriel Tamás (Budapesti Fazekas M. Gyak. Ált. Isk. és Gimn, 11. évf.) és

Seprődi Barnabás Bendegúz (Budapest, Óbudai Árpád Gimn., 10. évf.) dolgozata alapján