Feladat: B.5133 Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Bán-Szabó Áron ,  Duchon Márton ,  Fey Dániel ,  Kercsó-Molnár Anita ,  Kovács 129 Tamás ,  Kökényesi Márk Péter ,  Lőw László ,  Molnár-Szabó Vilmos ,  Nádor Benedek ,  Seres-Szabó Márton ,  Simon László Bence ,  Terjék András József ,  Varga Boldizsár ,  Virág Rudolf 
Füzet: 2021/november, 476 - 477. oldal  PDF  |  MathML 
Témakör(ök): Feladat, Térgeometriai bizonyítások
Hivatkozás(ok):Feladatok: 2020/november: B.5133

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A megoldáshoz használni fogjuk a következő jól ismert tételt, ami Erdős Pál nyomán Happy End-problémaként terjedt el. Azt mondjuk, hogy néhány pont a síkon általános helyzetű, ha nincs köztük három, ami illeszkedik egy egyenesre.

 
Tétel. Öt általános helyzetű pont közül a síkon mindig kiválasztható négy, amik egy konvex négyszög csúcsai (azaz konvex pozícióban vannak).
 

Bizonyítás. Legyenek az adott pontok X, Y, Z, V és W. Ha a pontok konvex burkának legalább négy csúcsa van, akkor az állítás nyilvánvaló. Feltehetjük tehát, hogy V és W az XYZ▵ belsejében van (lásd ábra).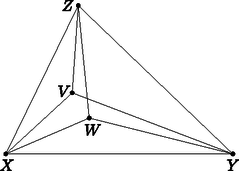
 
 
 

A W pont az XYV, XZV és YZV háromszögek közül pontosan egyben van benne, mondjuk W∈XYV▵, és így W∉XZV▵ valamint W∉YZV▵. Nyilvánvalóan V az XZW és YZW háromszögek közül legfeljebb (valójában pontosan) egyben van benne, vagyis feltehetjük, hogy V∉YZW▵.
Így Y, Z, V és W pontok konvex burkának Y és Z nyilvánvalóan csúcsa, míg W∉YZV▵ és V∉YZW▵ miatt csúcsa V és W is. Tehát Y, Z, V és W pontok valóban egy konvex négyszög csúcsai, ezzel a tétel állítását beláttuk.
Rátérünk a feladat megoldására. Tekintsünk egy olyan S síkot, ami a pontok által meghatározott egyenesek egyikével sem párhuzamos, és a pontok mindegyike a sík ugyanazon félterébe esik. Legyen A az adott pontok közül az S-hez legközelebbi (a feltevés szerint ez a pont egyértelmű), a további pontok B, C, D, E és F. Jegyezzük meg, hogy a konstrukció miatt az AB+, AC+, AD+, AE+ és AF+ félegyenesek egyike sem metszi az S síkot.
Vetítsük le centrálisan az A-tól különböző pontokat A-ból S-re, azaz legyen B'=S∩AB, C'=S∩AC, és így tovább. A Happy End-probléma miatt feltehetjük, hogy B'C'D'E' egy konvex négyszög, a B'D' és C'E' átlók metszéspontja legyen G. A vetítés mellett G pontnak a BD és CE szakaszokon is van őse, azaz létezik M∈BD¯ és N∈CE¯, amikre M'=N'=G. AM>AN az általánosság megszorítása nélkül feltehető, és így a konstrukció miatt N illeszkedik AM¯ szakaszra, azaz N az ABD háromszögnek is belső pontja.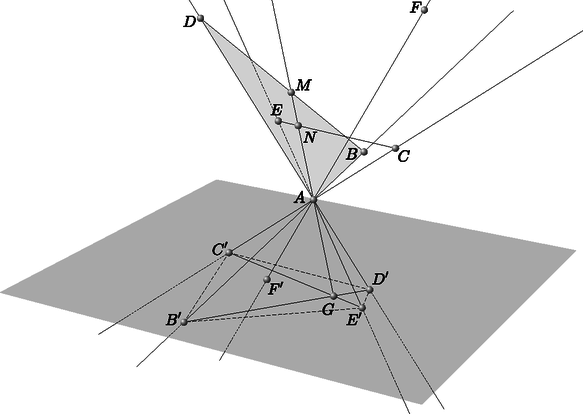
 
 
 

Kaptuk, hogy N=ABD▵∩CE¯, ami miatt nyilvánvalóan ABD és CEF háromszögek is metszik egymást. Ezzel az állítást beláttuk.
Nádor Benedek (Budapesti Fazekas M. Gyak. Ált. Isk. és Gimn., 10. évf.)