Feladat:	5336. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Kertész Balázs ,  Somlán Gellért ,  Téglás Panna ,  Tóth Ábel ,  Varga Vázsony
Füzet:	2021/november, 503 - 504. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Hullámterjedés 3 dimenzióban
Hivatkozás(ok):	Feladatok: 2021/május: 5336. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Megoldás. Jelöljük a repülő sebességét $v$-vel, a hangsebességet pedig $c$-vel. ($c\approx 340$ m/s.) A vadászgép szuperszonikus, vagyis $v>c$. A $v/c=\text{M}$ hányadost Mach-számnak nevezik (és néha Ma-val jelölik). Egy hangforrás által $t=0$ pillanatban kibocsátott hanghullám $t$ idő elteltével a forrástól $ct$ távolságra lévő pontokban halljuk meg. Ezek a pontok a térben egy $ct$ sugarú gömbfelületen helyezkednek el. A $v$ sebességgel mozgó hangforrás hangja $t=0$ pillanatban olyan pontokba érkezik el, amelyek tetszőleges $\Delta t$ idővel korábban indultak el. Ezek a hullámok $v\Delta t$ távolsággal ,hátrábbról'' indultak és $c\Delta t$ sugarú gömbfelületig jutottak el (1. ábra). Ezen gömbfelületek határa (burkolója) egy $\alpha =\text{arcsin}\frac{c}{v}$ félnyílásszögű kúpfelület. Ezt a felületet Mach-kúpnak nevezik, amelyre 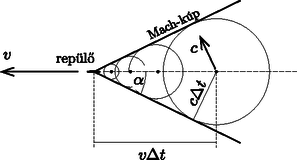$\begin{array}{c}{\displaystyle \text{sin}\alpha =\frac{1}{\text{M}}\mathrm{.}}\end{array}$   1. ábra   A vadászgép sebességének kiszámításához az $\alpha$ szöget kell meghatároznunk. Mivel a vadászgép a mező síkjával párhuzamosan repül, a három megfigyelőnek egy hiperbolán (a Mach-kúp síkmetszetén) kell elhelyezkednie. Válasszunk egy olyan koordináta-rendszert, amelynek $x$ tengelye a vadászgép sebességével párhuzamos, a $z=0$ sík a mező síkja. A koordináta-rendszer origója legyen annál az $A$ megfigyelőnél, amelyiknek éppen a feje felett repült el a vadászgép. A másik két megfigyelő ($B$ és $C$) az $x$ ‐ $z$ síkra szimmetrikusan helyezkedik el, koordinátáik a megadott (km-ben mért) távolságadatok szerint: $B\left(\sqrt[]{147}\mathrm{,7,0}\right)$, $C\left(\sqrt[]{147}\mathrm{,}-\mathrm{7,0}\right)$. A három megfigyelő helyzetét az $x$ ‐ $y$ síkban a 2. ábra mutatja. 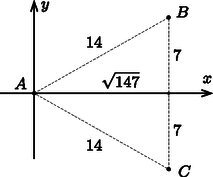  2. ábra   Legyen $B$ és $C$ felezőpontja $F$. A Mach-kúpnak a tengelyére merőleges síkmetszetei körök. A $B$ és $C$ pontokra illeszkedő kör középpontja legyen $K$, a mező alatt legmélyebben található pontja pedig $L$. A 3. ábra ezt a kört mutatja az $x=\sqrt[]{147}$ síkban. Innen leolvashatjuk, hogy a kör sugara 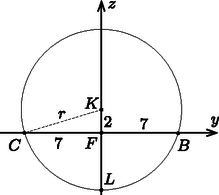$\begin{array}{c}{\displaystyle r=\sqrt[]{7^2+2^2}=\sqrt[]{53}\approx 7\mathrm{,}\mathrm{28,}}\end{array}$ az $L$ pont $z$ koordinátája pedig $\begin{array}{c}{\displaystyle z_L=2-r\approx -5\mathrm{,}28.}\end{array}$   3. ábra   Ábrázoljuk most a három megfigyelő helyét, a repülő útvonalát és a Mach-kúpot az $x$ ‐ $z$ síkra vetítve (4. ábra). 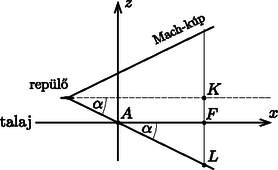  4. ábra   Az ábráról leolvashatjuk, hogy $\begin{array}{c}{\displaystyle \text{tg}\alpha =\frac{FL}{AF}=\frac{5\mathrm{,}28}{\sqrt[]{147}}\approx 0\mathrm{,}\mathrm{435,}\text{tehát}\alpha =23\mathrm{,}{5}^{\circ }\mathrm{.}}\end{array}$ Ezek szerint $\begin{array}{c}{\displaystyle \text{M}=\frac{c}{v}=\frac{1}{\text{sin}\alpha }=2\mathrm{,}\mathrm{5,}}\end{array}$ és így a vadászgép sebessége: $\begin{array}{c}{\displaystyle v=2\mathrm{,}5c\approx 850\frac{\text{m}}{\text{s}}\mathrm{.}}\end{array}$