Feladat: 1969. évi Nemzetközi Matematika Diákolimpia 22. feladata Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Ferró J. ,  Füredi Zoltán ,  Győry György ,  Göndőcs Ferenc ,  Komjáth Péter ,  Pressing Lajos ,  Reviczky János ,  Török I. 
Füzet: 1970/december, 215 - 217. oldal  PDF  |  MathML 
Témakör(ök): Kombinatorikus geometria síkban, Kombinációk, Nemzetközi Matematikai Diákolimpia
Hivatkozás(ok):Feladatok: 1969/szeptember: 1969. évi Nemzetközi Matematika Diákolimpia 22. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Nézzük meg először, mit állít a feladat a legkisebb megengedett n-re, 5-re. Ekkor (5-32)=1, azt kell tehát belátnunk, hogy ha adott a síkban 5 pont, melyek közül semelyik 3 sem esik egy egyenesbe, akkor van legalább 1 olyan konvex négyszög, melynek csúcspontjai az adott pontok közül valók.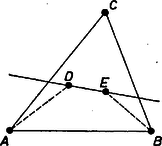
Az 5 pont helyzetére vonatkozólag 3 lényegesen különböző esetet kell megvizsgálnunk: az öt pont konvex burka: 1. ötszög, 2. négyszög, 3. háromszög. (Véges sok adott pont konvex burka az a konvex sokszög, melynek csúcsai az adott pontok közül valók és amely tartalmazza az összes többi pontot.)
Az 1. és 2. esetben tulajdonképpen készen vagyunk. Az 1. esetben bármelyik pontot elhagyva, a fennmaradó 4 pont konvex négyszöget alkot. A 2. esetben megfelel maga a konvex burok.
Ha pedig a konvex burok háromszög, akkor így okoskodunk: jelöljük e háromszög csúcsait A, B, C-vel, a másik két pont legyen D és E (1. ábra).

 
 
1. ábra
 

A konvex burok definíciója szerint D és E a háromszögön belül van, és mivel semelyik három pont nem esik egy egyenesbe, nem lehetnek az oldalegyeneseken sem. Ez utóbbiból az is következik, hogy a DE egyenes nem mehet át A, B, C egyikén sem. Ezért a DE egyenes által meghatározott 2 félsík egyike kettőt tartalmaz A, B és C közül a belsejében, legyenek ezek A és B. Ekkor az ADEB négyszög konvex, hiszen az előbbiek szerint az ADE, DEB szögek kisebbek 180∘-nál, és ez áll a DAB és EBA szögre is, mert ez utóbbiak az eredeti háromszög szögeinek részei.
Ezzel n=5-re az állítást beláttuk.
Ha az adott n pont közül tetszés szerint kiválasztunk ötöt, akkor a fentiek szerint van olyan konvex négyszög, melynek csúcspontjai a kiválasztott 5 pont közül valók. Kiválasztva minden lehetséges módon 5 pontot, minden ilyen kiválasztáshoz tartozik az előbbiek szerint legalább egy konvex négyszög. Ezen kiválasztások száma nyilván (n5). Előfordulhat azonban, hogy különböző kiválasztásokhoz ugyanaz a konvex négyszög tartozik. Nézzük meg ezért fordítva, hogy egy rögzített konvex négyszög hány kiválasztáshoz tartozik hozzá. Annyihoz, ahányféleképpen az ötödik pont a rögzített négy pont mellé megválasztható: (n-4)-féleképpen. Ezért a konvex négyszögek száma legalább (n5)⋅1n-4=(n4)⋅15.
Ezután már csak azt kell megmutatnunk, hogy
15(n4)≥(n-32),
hacsak n≥5. A két oldalt részletesen kiírva:
15(n4)=15!n(n-1)(n-2)(n-3),(n-32)=(n-3)(n-4)2,
elég tehát megmutatni, hogy
n(n-1)(n-2)(n-3)(n-3)(n-4)≥5!2=60.(1)

Egyszerűsítsünk (n-3)-mal és írjuk az (n-2)(n-4) hányados helyére a nála kisebb 1-et. Az így adódó n(n-1)≥60 teljesül minden n≥9-re, mert (n-1)2<n(n-1) és már 82≥60. A kimaradt n=5, 6, 7, 8-ra pedig pontos számítással adódik, hogy n=5, 6-ra (1)-ben egyenlőség, n=7, 8-ra pedig már az állítás szerinti egyenlőtlenség áll fenn.
 

Szabó György

 

II. megoldás. A bizonyítandó formula egy binomiális együttható, melynek kombinatorikus jelentése az (n-3) pont közül kiválasztható pontpárok száma. A feladatban azonban n pont szerepel, tehát valamilyen meggondolással 3 pont a többitől elkülönítendő. Ebből adódik a következő ötlet.
Rögzítsünk az n pontból egyelőre tetszés szerint hármat. Próbáljuk kimutatni, hogy a fennmaradó (n-3) pontból akárhogy választunk ki még 2 pontot, létezik olyan konvex négyszög, melynek csúcsai az utóbb kiválasztott 2 pont, és a rögzített 3 pont közül 2. Bizonyítás közben ki fog derülni, hogy a rögzítendő 3 pont kiválasztására vonatkozólag kell-e további feltevés, és ha igen, akkor milyen. Ha pedig a fenti állítást sikerül belátni, akkor nyilván készen vagyunk, mert az (n-3) pont közül való 2 pont különböző kiválasztásaihoz különböző konvex négyszögek fognak tartozni, ezt biztosítja az a kikötés, hogy a konvex négyszög 2 csúcsa mindig a kiválasztott 2 pont legyen.
Legyen a 3 rögzített pont A, B, C, a két kiválasztott pont pedig P és Q. Ha A, B, C, P, Q konvex burka ötszög, akkor A, B és C bármelyikét elhagyva a maradó 4 pont megfelelő konvex négyszöget alkot.
Ha A, B, C, P, Q konvex burka négyszög, és ennek csúcsai között P is, Q is szerepel, akkor ezzel az esettel is készen vagyunk. Ha viszont P és Q közül csak az egyik, mondjuk P szerepel a 4 csúcs között, akkor rajzoljuk be a konvex buroknégyszög átlóit, vegyük a kapott 4 háromszög közül azt, amelyik tartalmazza Q-t (2. ábra, ennek kiválasztása egyértelmű, hiszen Q nem lehet rajta átlón). E háromszögnek 2 csúcsa adott pont, így legalább egyikük A, B és C közül való. Ezt, ill. a 2 egyikét elhagyva Q a maradt három ponttal konvex négyszöget feszít ki, és csúcsai közt van 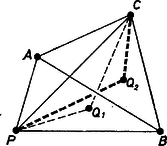P is.
 
 
2. ábra
 

Ha végül az A, B, C, P, Q pontok konvex burka háromszög, akkor közülük 2 a háromszög belsejében van. Összekötő egyenesük a háromszöget kettévágja, nem megy át annak egyik csúcsán sem, és így az egyenes valamelyik partjára 2 csúcspont kerül. E 2 pont és a 2 belső pont ‐ mint az I. megoldásban láttuk ‐ konvex négyszöget alkot, a háromszögnek az egyenes másik partjára esett csúcsa nem szerepel a konvex négyszögünk csúcsai között, és előfordulhat, hogy ez a kimaradó csúcs éppen a kiválasztott P vagy Q.
Az ilyen eset elkerülhető, ha A-t, B-t és C-t az adott n pont konvex burkának csúcspontjai közül választjuk (a burok csúcsainak száma legalább 3). Megmutatjuk ugyanis, hogy ha A, B és C ilyen megválasztása után az A, B, C, P, Q pontok konvex burka háromszög, akkor ennek csúcsai A, B és C, tehát a mondott eset nem következhet be.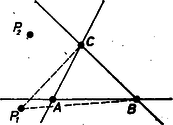
 
 
3. ábra
 

Valóban, ekkor P és Q csak az ABC háromszög belsejében lehet, mert nem lehet a háromszög egy belső szögének csúcsszögtartományában (3. ábra P1) ‐ különben e tartomány csúcsa nem lenne csúcsa az n pont konvex burkának ‐, és nem lehet a háromszög oldalához csatlakozó síkrészben sem (3. ábra P2), különben az 5 pont konvex burka nem háromszög volna.
Ezzel ‐ az előrebocsátottak szerint ‐ az állítást bebizonyítottuk.
 

Győry György