Kezdőlap


Feladat:	5229. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bonifert Balázs
Füzet:	2021/január, 46 - 47. oldal		PDF \| MathML
Témakör(ök):	Feladat, Coulomb-törvény, Egyéb (tömegpont mozgásegyenletével kapcsolatos)
Hivatkozás(ok):	Feladatok: 2020/április: 5229. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$a)$ Az ábra jelöléseit használva kiszámíthatjuk, hogy az $F$ erő nagysága:

\begin{matrix} F = k \frac{Q q}{d^{2}} = k \frac{Q q}{R^{2} + L^{2}} . \end{matrix}

Az erők ,,vízszintes'' komponensei kiejtik egymást, a ,,függőlegesek'' pedig összeadódnak. Az ábrán

α

-val jelölt szög koszinusza: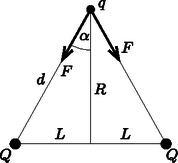

\begin{matrix} cos α = \frac{R}{d} = \frac{R}{\sqrt[]{R^{2} + L^{2}}} . \end{matrix}

A körpályán egyenletesen keringő test mozgásegyenlete:

\begin{matrix} m a = F_{eredő} = 2 F cos α = 2 k \frac{Q q R}{{(R^{2} + L^{2})}^{\frac{3}{2}}} . \end{matrix}

Mivel az

m

tömegű test állandó

v

nagyságú sebességgel körpályán mozog, a keringési ideje kiszámolható a gyorsulásából:

\begin{matrix} T = \frac{2 π R}{v} és a = \frac{v^{2}}{R}, \end{matrix}

ahonnan a keringési idő:

\begin{matrix} T = 2 π \sqrt[]{\frac{m}{2 k Q q}} {(R^{2} + L^{2})}^{\frac{3}{4}} . \end{matrix}

b)

R ≪ L

esetben a keringési idő kifejezése így közelíthető:

\begin{matrix} T = 2 π \sqrt[]{\frac{m}{2 k Q q}} L^{\frac{3}{2}} {(\frac{R^{2}}{L^{2}} + 1)}^{\frac{3}{4}} \approx 2 π \sqrt[]{\frac{m}{2 k Q q}} L^{\frac{3}{2}} (1 + \frac{3}{4} \frac{R^{2}}{L^{2}}) . \end{matrix}

R

-et elhanyagoljuk

L

mellett, akkor

\begin{matrix} T = 2 π \sqrt[]{\frac{m}{2 k Q q}} L^{\frac{3}{2}} . \end{matrix}

Ebben a közelítésben a keringési idő nem függ a körpálya sugarától.

R ≫ L

esetén

\begin{matrix} T = 2 π \sqrt[]{\frac{m}{2 k Q q}} R^{\frac{3}{2}} {(\frac{L^{2}}{R^{2}} + 1)}^{\frac{3}{4}} \approx 2 π \sqrt[]{\frac{m}{2 k Q q}} R^{\frac{3}{2}} (1 + \frac{3}{4} \frac{L^{2}}{R^{2}}) . \end{matrix}

L

-et elhanyagoljuk

R

mellett, akkor

\begin{matrix} T = 2 π \sqrt[]{\frac{m}{2 k Q q}} R^{\frac{3}{2}} . \end{matrix}

Ebben a közelítésben a keringési idő nem függ a

Q

nagyságú töltések távolságától.

c)

A rezgő test mozgásegyenlete:

\begin{matrix} m a (x) = 2 F cos α = 2 k \frac{Q q x}{{(x^{2} + L^{2})}^{\frac{3}{2}}}, \end{matrix}

ahol

a (x)

a test pillanatnyi gyorsulását jelöli abban a helyzetben, ahol a test

x

távolságban van

Q

töltések felezőpontjától (vagyis az egyensúlyi helyzetétől).
Látható, hogy a mozgás nem egyenletesen gyorsuló, hiszen

a (x) \neq állandó

, de nem is harmonikus rezgőmozgás, mert

a (x)

nem arányos

x

-szel. A mozgás időbeli leírása meglehetősen bonyolult, elemi eszközökkel nem adható meg, és emiatt a rezgés idejét sem tudjuk pontosan kiszámítani. De erre nincs is szükségünk, a rezgésidőt csak a keringés idejével akarjuk összehasonlítani.
Tudjuk, hogy a mozgás során minden pillanatban

R^{2} \geq x^{2}

(és a mozgás fordulópontjait leszámítva határozott egyenlőtlenség áll fenn), ezért ha a mozgásegyenletben a tört nevezőjében az

x^{2}

-et

R^{2}

-tel helyettesítjük, akkor (az

x = \pm R

pontokat leszámítva) az erőt megadó kifejezés kisebb lesz az eredetinél:

\begin{matrix} 2 k \frac{Q q x}{{(x^{2} + L^{2})}^{\frac{3}{2}}} > 2 k \frac{Q q x}{{(R^{2} + L^{2})}^{\frac{3}{2}}} . \end{matrix}

Az egyenlőtlenség jobb oldalának megfelelő erőtörvény egy harmonikus rezgőmozgást ír le, és ezen rezgés periódusideje éppen a körmozgáséval egyenlő. Mivel a tényleges rezgés ,,rugóállandója'' ennél az állandónál nagyobb, a kialakuló rezgés periódusideje kisebb lesz, mint a keringésé.

Bonifert Balázs (Budapest, Baár-Madas Ref. Gimn., 11. évf.)