Kezdőlap


Feladat:	717. fizika gyakorlat	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Schneider Dávid
Füzet:	2021/január, 44 - 45. oldal		PDF \| MathML
Témakör(ök):	Gyakorlat, Egyenletes mozgás (Egyenes vonalú mozgások), Visszhang
Hivatkozás(ok):	Feladatok: 2020/október: 717. fizika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Rajzoljuk le a denevér repülési útvonalát és a barlang falát (1. ábra). Az ultrahang a $D_{1}$ pontból indul ki, és a falról visszaverődve a $D_{2}$ pontban érkezik vissza a denevérhez. Az ábrán látható $d = D_{1} D_{2} = 5, 4$ m az a távolság, amit a denevér a megadott idő alatt a megadott sebességgel megtesz.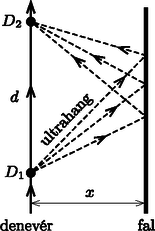
A hang a denevértől kiindulva különböző irányokban terjed, és a barlang faláról különböző irányokban verődik vissza. A denevér azt a hangot hallja meg legelőször, amelyik a legrövidebb idő alatt, tehát a legrövidebb utat megtéve jut vissza hozzá.

1. ábra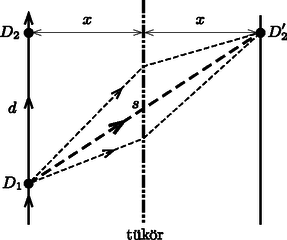

2. ábra

Tükrözzük a

D_{2}

pontot a barlang falának síkjára (2. ábra). A különböző irányban haladó hanghullámok teljes útjának hossza megegyezik a

D_{1}

-et

D_{2}'

-vel összekötő, a fal (a tükör) síkjánál esetleg megtörő szakaszok együttes hosszával. Ezek közül a

D_{1} D_{2}'

egyenes szakasz a legrövidebb, és ennek hossza az a távolság, amennyit az ultrahang a megadott

t

idő alatt megtesz:

\begin{matrix} s = v_{hang} \cdot t = 333 \frac{m}{s} \cdot 0, 120 s = 39, 96 m . \end{matrix}

D_{1} D_{2} D_{2}'

derékszögű háromszögre felírt Pitagorasz-tétel alapján

\begin{matrix} 2 x = \sqrt[]{s^{2} - d^{2}} \approx 39, 6 m, \end{matrix}

a denevér és a barlang falának távolsága tehát

x \approx 19, 8 m

Schneider Dávid (Zalaegerszeg, Zrínyi M. Gimn., 10. évf.)

Megjegyzések. 1. Ugyanezt az eredményt úgy is megkaphatjuk, ha feltételezzük, hogy az ultrahang a síktükörhöz érkező fényhez hasonlóan verődik vissza, vagyis a beesési szög megegyezik a visszaverődés szögével. Ez akkor igaz, ha a barlang fala elegendően ,,sima", a sík felülettől legfeljebb az ultrahang hullámhosszának megfelelő mértékben tér csak el.
2. Sok versenyző indokolatlan pontossággal (pl. x = 19,813 344 m-nek) adta meg a denevér útvonalának és a barlang falának távolságát. Ennek nem sok értelme van, hiszen a denevér fülének mérete és a barlang falának göcsörtössége sok-sok nagyságrenddel felülmúlja a megadott szám utolsó számjegyeinek megfelelő távolságokat. A fizikai mennyiségek kiszámított értékét annyi számjegy pontossággal szabad csak megadni, amennyit komolyan vehetünk. Ez a pontosság nem haladhatja meg a feladat szövegében megadott bemenő adatok pontosságát. (A szerk.)