Kezdőlap


Feladat:	B.5015	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Stomfai Gergely
Füzet:	2020/november, 475 - 476. oldal		PDF \| MathML
Témakör(ök):	Feladat, Körülírt kör, Síkgeometriai számítások trigonometria nélkül, Háromszögek geometriája
Hivatkozás(ok):	Feladatok: 2019/március: B.5015

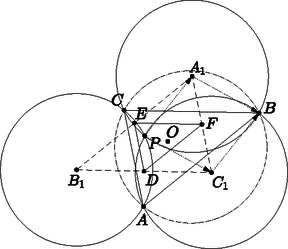
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen a három kör középpontja $A_{1}$ , $B_{1}$ és $C_{1}$ , a közös pontjuk pedig $P$ az ábra szerint.

Megmutatjuk, hogy az

A A_{1}

B B_{1}

C C_{1}

szakaszok felezőpontjai egybeesnek (

O

pont). Irányítsunk a közös

P

pontból a körök középpontjaiba helyvektorokat:

\vec{P A_{1}} = a

\vec{P B_{1}} = b

\vec{P C_{1}} = c

. (Az ábrán csak a

\vec{P A_{1}}

és

\vec{P C_{1}}

vektorokat tüntettük fel.) Ezek egységnyi hosszúságúak. Az

A_{1} B

C_{1} B

C_{1} A

B_{1} A

B_{1} C

A_{1} C

is mind egységnyiek, így

\begin{matrix} a + c = \vec{P B}, a + b = \vec{P C}, b + c = \vec{P A} . \end{matrix}

A A_{1}

szakasz felezőpontjába mutató helyvektor:

\begin{matrix} \frac{\vec{P A_{1}} + \vec{P A}}{2} = \frac{a + b + c}{2} . \end{matrix}

Ugyanezt a vektort kapjuk

B B_{1}

és

C C_{1}

felezőpontjára is, a három felezőpont valóban egybeesik. Az

A_{1} B_{1} C_{1}

háromszög

O

-ra vonatkozó tükörképe az

A B C

háromszög. Mivel az

A_{1} B_{1} C_{1}

háromszög köré a

P

körül egységnyi sugarú kör írható, ezért tükörképe, az

A B C

háromszög köré is.

Stomfai Gergely (Budapest, ELTE Apáczai Cs. J. Gyakorló Gimn. és Koll., 10. évf.) dolgozata alapján

Megjegyzés. A megoldásból is látható, hogy az

O

pont az

A_{1} B_{1} C_{1}

háromszög Feuerbach-körének középpontja, a

P

pont a köréírt körének középpontja, a

P

pont

O

-ra vonatkozó tükörképe, pedig az

A_{1} B_{1} C_{1}

háromszög magasságpontja, amely, mint megtudtuk az

A B C

háromszög köréírt körének középpontja. Ezt úgy is fogalmazhatjuk, hogy az

A_{1} B_{1} C_{1}

háromszög

D E F

talpponti háromszögét a körérírt kör

P

középpontjából a kétszeresére nagyítottuk, így kaptuk az

A B C

háromszöget.