Kezdőlap


Feladat:	5221. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Horváth Anikó
Füzet:	2020/november, 498 - 500. oldal		PDF \| MathML
Témakör(ök):	Feladat, Egyéb kényszermozgás
Hivatkozás(ok):	Feladatok: 2020/április: 5221. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az autó hurkon való áthaladásának kritikus pontja a pálya legfelső pontja. Ha itt a nyomóerő éppen nullára csökken, akkor még nem válik el az autó a pályától. A körmozgás feltétele, hogy a testre ható erők eredője létrehozza a centripetális gyorsulást. Ha a játékautó sebessége a pálya legfelső pontjában $v_{1}$ , akkor határesetben (amikor a test még éppen nem válik el a kör alakú pályától):

\begin{matrix} m g = m \frac{v_{1}^{2}}{r}, tehát v_{1}^{2} = r g . \end{matrix}

A folyamat során a disszipatív erők hatása elhanyagolható, így a mechanikai energia megmarad.

\begin{matrix} \frac{1}{2} m v^{2} = 2 m g r + \frac{1}{2} m v_{1}^{2} = 2 m g r + \frac{1}{2} m g r = \frac{5}{2} m g r, \end{matrix}

vagyis

\begin{matrix} v = \sqrt[]{5 r g} . \end{matrix}

Az autó a körmozgás második negyedében tud leválni a pályájáról (előtte ‐ nem elegendően nagy kezdősebességnél ‐ csak visszacsúszna a körvíven). Legyen a leváláskor a játékautó sebessége

u

, a hozzá húzott sugár függőlegessel bezárt szöge

α

(lásd az ábrát). Ekkor még éppen körpályán halad (a pálya nyomóereje már éppen nullára csökkent), így a mozgásegyenlet sugár irányú komponense: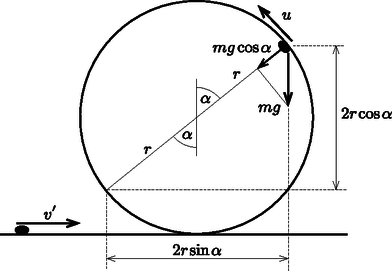

\begin{matrix} m g cos α = m \frac{u^{2}}{r}, vagyis u^{2} = r g cos α . \end{matrix}

A szemközti pontba való becsapódásáig mozgása ferde hajítás.
Vízszintesen:

\begin{matrix} 2 r sin α = u_{x} t = u t cos α, azaz t = \frac{2 r sin α}{u cos α} . \end{matrix}

Függőlegesen:

\begin{matrix} 2 r cos α = \frac{g}{2} t^{2} - u t sin α . \end{matrix}

t

-re és

u^{2}

-re kapott kifejezések behelyettesítésével, majd

2 r

-rel egyszerűsítve kapjuk:

\begin{matrix} cos^{4} α + sin^{2} α cos^{2} α - sin^{2} α = 0. \end{matrix}

Innen (a trigonometrikus Pitagorasz-tételt kihasználva):

\begin{matrix} cos^{4} α + cos^{2} α - cos^{4} α - 1 + cos^{2} α = 0, cos^{2} α = \frac{1}{2}, cos α = \frac{1}{\sqrt[]{2}}, \end{matrix}

tehát

\begin{matrix} α = 45^{\circ} . \end{matrix}

Az energiamegmaradás törvénye szerint:

\begin{matrix} \frac{1}{2} m v'^{2} & = (1 + cos α) m g r + \frac{1}{2} m u^{2}, \\ v'^{2} & = (2 + \sqrt[]{2}) r g + r g \frac{1}{\sqrt[]{2}}, \\ v' & = \sqrt[]{(2 + \frac{3 \sqrt[]{2}}{2}) r g}, \end{matrix}

és végül a keresett arány:

\begin{matrix} \frac{v'}{v} = \sqrt[]{\frac{2}{5} + \frac{3 \sqrt[]{2}}{10}} \approx 0, 91. \end{matrix}

Horváth Anikó (Szeged, Radnóti M. Kís. Gimn., 11. évf.)