Kezdőlap


Feladat:	B.4979	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Kocsis Anett , Tóth Balázs , Tubak Dániel
Füzet:	2020/október, 409 - 412. oldal		PDF \| MathML
Témakör(ök):	Feladat, Síkgeometriai bizonyítások, Húrnégyszögek
Hivatkozás(ok):	Feladatok: 2018/október: B.4979

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen a $B C$ egyenes és az $A E B ▵$ köréírt körének $B$ -től különböző metszéspontja 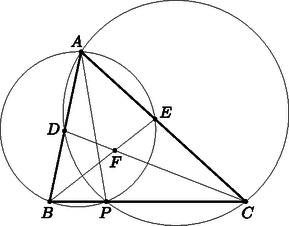$P$ .

C

pontnak erre a körre vonatkozó hatványa

C P \cdot B C = C E \cdot C A

.
Tudjuk, hogy

B C^{2} = B D \cdot B A + C E \cdot C A

. Utóbbi egyenletből kivonva előbbit, azt kapjuk, hogy

\begin{matrix} B C \cdot (B C - C P) = B D \cdot B A . \end{matrix}

Viszont

B C - C P = B P

, így

B P \cdot B C = B D \cdot B A

.
Az egyenlet jobb oldala a

B

pontnak az

A D C ▵

köréírt körére vonatkozó hatványa. Ezek szerint az egyenlőség miatt

P

rajta van az

A D C ▵

köréírt körén is.
Legyen

A P C ∢ = φ

. Ekkor kerületi szögek egyenlősége miatt az

A D P C

körön

A D C ∢ = A P C ∢ = φ

. Tudjuk, hogy

A P B ∢ = 180^{\circ} - φ

. Az

A B P E

körön a kerületi szögek miatt

A E B ∢ = A P B ∢ = 180^{\circ} - φ

. Így

A D F ∢ = A D C ∢ = φ

és

A E F ∢ = A E B ∢ = 180^{\circ} - φ

, mivel

D

F

C

, illetve

E

F

B

egy egyenesen vannak. Ezek szerint

A D F ∢ + A E F ∢ = 180^{\circ}

, tehát

A D F E

valóban húrnégyszög, hiszen két szemközti szögének összege

180^{\circ}

.
Diszkusszió: Akkor lehetne probléma az ábrával ‐ és így a bizonyítással is ‐, hogyha az

A E B ▵

köréírt köre érinti

B C

-t, vagy pedig a

B C

szakaszon kívül metszi másodszor. A

C

-ből felírt hatvány a körre ekkor is helyes lesz, így

C E \cdot C A = C P \cdot B C

teljesülni fog. Hogyha a

B C

szakaszon kívül metszi a kör az egyenest, az csak

B

-n túl lehet, így ha

P

,,rossz'' helyen van, akkor

C P \geq B C

teljesülni fog. Ennek alapján

C P \cdot B C \geq B C^{2}

, így a

B C^{2} = B D \cdot B A + C E \cdot C A

egyenletben

B D \cdot B A \leq 0

, ami nyilvánvalóan nem lehetséges, mert ekkor

D

nem belső pontja lenne az

A B

oldalnak. Ezek szerint a feltétel alapján a

P

pont a

B C

szakasz belső pontja, az ábra mindig megfelelő, és a bizonyítás helyes.

Tóth Balázs (Budapesti Fazekas M. Gyak. Ált. Isk. és Gimn., 11. évf.) dolgozata alapján

II. megoldás. Legyen az

A B C

háromszög

A

-nál fekvő belső szöge

α

, a

B

-ből, illetve

C

-ből induló magasságvonalak talppontjai pedig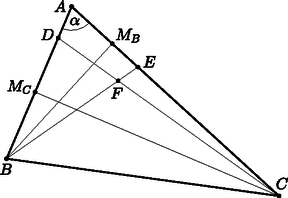

M_{B}

és

M_{C}

B C

oldalra felírt koszinusztételből:

\begin{matrix} B C^{2} = B A^{2} + C A^{2} - 2 \cdot B A \cdot C A \cdot cos α, \end{matrix}

(1)

valamint a feltétel szerint:

\begin{matrix} B C^{2} = C A \cdot C E + B D \cdot B A . \end{matrix}

(2)

(1) és (2) különbségéből:

\begin{matrix} 0 & = C A (C A - C E) + B A (B A - B D) - 2 \cdot B A \cdot C A \cdot cos α, \\ 0 & = A E \cdot C A + A D \cdot B A - 2 \cdot B A \cdot C A \cdot cos α . \end{matrix}

Rendezés után:

\begin{matrix} 2 cos α = \frac{A E}{B A} + \frac{A D}{C A} . \end{matrix}

(3)

Másrészt az

A C M_{C}

és

A B M_{B}

derékszögű háromszögekből

cos α

-t kifejezve:

\begin{matrix} 2 cos α = \frac{M_{C} A}{C A} + \frac{M_{B} A}{B A} . \end{matrix}

(4)

(3) és (4) különbsége alapján:

\begin{matrix} \frac{A E - M_{B} A}{A B} & = \frac{M_{C} A - A D}{A C}, \\ \frac{E M_{B}}{A B} & = \frac{D M_{C}}{A C} . & (5) \end{matrix}

Átrendezés után

sin α

-val bővítve:

\begin{matrix} \frac{D M_{C}}{E M_{B}} = \frac{A C}{A B} = \frac{A C \cdot sin α}{A B \cdot sin α} = \frac{C M_{C}}{B M_{B}} . \end{matrix}

Ez azt jelenti, hogy a

D M_{C} C

és

E M_{B} B

derékszögű háromszögek hasonlóak, a megfelelő szögek egyenlők:

M_{C} D C ∢ = M_{B} E B ∢

. Mivel

M_{B} E B ∢ = A E F ∢

, és az

M_{C} D C ∢

mellékszöge

F D A ∢

, így

\begin{matrix} A E F ∢ + F D A ∢ = 180^{\circ}, \end{matrix}

azaz

A E F D

valóban húrnégyszög.
Ha a

D

és

M_{C}

pontok egybeesnek, akkor (5) miatt az

E

és

M_{B}

pontok is egybeesnek, az

A D F E

négyszög két szemközti szöge derékszög, tehát ekkor is húrnégyszöget kapunk.

Kocsis Anett (Győr, Révai Miklós Gimn., 11. évf.)

III. megoldás. Tekintsük a

B

középpontú,

\sqrt[]{B D \cdot B A} = r_{1}

sugarú

c

; és a

C

középpontú,

\sqrt[]{C E \cdot C A} = r_{2}

sugarú

d

köröket. Ezekre a körökre invertálva az

A

pontot kapjuk a

D

és az

E

pontot, mivel úgy választottuk meg a sugarakat, hogy ez teljesüljön.
A feladatban szereplő feltétel szerint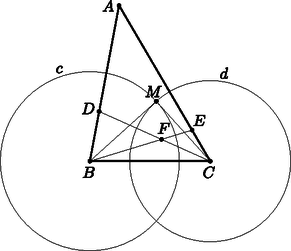

\begin{matrix} B C^{2} = B D \cdot B A + C E \cdot C A = r_{1}^{2} + r_{2}^{2}, \end{matrix}

tehát a Pitagorasz‐tétel megfordítása értelmében a

B C M

háromszög derékszögű, vagyis a két kör bezárt szöge (ami a metszéspontjukba húzott érintők bezárt szöge)

90^{\circ}

. Ebben az esetben, ha valamelyik körre invertáljuk a másik kört, akkor annak a képe önmaga lesz, tehát invariáns alakzat. Ezeket felhasználva láthatjuk, hogy ha

D

-t invertáljuk a

d

, valamint

E

-t a

c

körre, akkor képeiknek egybe kell esniük, ez pedig csak a két egyenes metszéspontjában lehetséges, amit az ábrán

F

-fel jelöltünk.

Látható, hogy ebben az esetben

B D \cdot B A = r_{1}^{2} = B F \cdot B E

, azaz a

B D F

és

B A E

háromszögek hasonlók, tehát

D F B ∢ = B A E ∢

.
Ekkor az

A D F E

négyszög valóban húrnégyszög lesz, hiszen a szemközti szögeinek összege

180^{\circ}

. Ezzel állításunkat beláttuk.

Tubak Dániel (Szegedi Radnóti M. Kísérleti Gimn., 11. évf.)

Megjegyzés. A megoldás csak a következő tétel alkalmazásával teljes: Két inverzió sorrendje pontosan akkor cserélhető fel, ha az alapkörök merőlegesen metszik egymást.
Esetünkben az

A

pont

c

körre vonatkozó inverze a

D

pont, majd ennek a

d

-re vonatkozó inverze rajta van a

C D

egyenesen. Másrészt az

A

pont

d

-re vonatkozó inverze az

E

pont, majd ennek inverze a

c

-re a

B E

egyenesen van. Ha a két inverzió felcserélhető, akkor valóban csak a két egyenes metszéspontja, az

F

pont lehet a közös kétszeres inverz.
Vázoljuk az inverziók sorrendjére vonatkozó tétel bizonyítását.
Az inverzió szögtartó. Ebből következően az inverzió inverziótartó: ha

P

és

Q

egymás képei az

i

körre való inverziónál, és

P'

Q'

i'

ezek képei a

j

körre való inverziónál, akkor

P'

és

Q'

egymás képei az

i'

-re való inverziónál. Valóban,

P

és

Q

pontosan akkor egymás képei

i

-nél, ha a

P

-n is és

Q

-n is átmenő körök valamennyien merőlegesek

i

-re ‐ ez a tulajdonság pedig megmarad, ha

j

-re invertálunk.
Tehát ha az

i_{1}

i_{2}

körökre való inverziók kommutativitását vizsgáljuk, akkor áttranszformálhatjuk őket egy inverzióval, a transzformációk megmaradnak, kommutativitásuk ott is vizsgálható.
Két metsző körre vonatkozó inverzió két metsző egyenesre vonatkozó tükrözéssé változik, ha a két kör metszéspontja körüli inverziót alkalmazunk.
A szögtartás miatt akkor és csak akkor cserélhető fel a tükrözések sorrendje, ha a két egyenes merőleges egymásra.