Feladat: 1967. évi Nemzetközi Matematika Diákolimpia 11. feladata Korcsoport: 16-17 Nehézségi fok: nehéz
Füzet: 1968/április, 149 - 150. oldal  PDF  |  MathML 
Témakör(ök): Szögfüggvények, síkgeometriai számítások, Nemzetközi Matematikai Diákolimpia, Lefedések, Paralelogrammák
Hivatkozás(ok):Feladatok: 1967/szeptember: 1967. évi Nemzetközi Matematika Diákolimpia 11. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. A feladat feltételei közül egyelőre csak annyit használunk fel, hogy α hegyesszög. Így az ABC háromszögben B-nél tompaszög van, az AB és BC szakaszok felező merőlegesei a háromszögön kívül metszik egymást, az AC oldalt az előbbi A-hoz közelebb, az utóbbi C-hez közelebb metszi (1. ábra).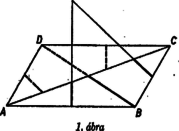

 

 

Ez a két felező merőleges tehát olyan három részre vágja az ABC háromszöget, hogy mindegyik rész belső pontjaihoz az illető rész által tartalmazott csúcs van a háromszög csúcsai közül a legközelebb. A BD szakasznak a háromszögbe eső része a B-hez tartozó részben fut, mert végpontja egyenlő távolságra van A-tól és C-től. Hasonló állítás igaz az ACD háromszögre is, így az ABD háromszög pontjaihoz az A, B, C, D pontok közül az A, B, D csúcsok valamelyike van legközelebb ‐ elegendő tehát annak a szükséges és elegendő feltételét megvizsgálnunk, hogy az ABD háromszöget a KA, KB; KD körök lefedjék. Két esetet különböztetünk meg aszerint, hogy α 60∘-nál kisebb-e vagy nagyobb. Ha 0<α≤60∘, a KA körnek a BAD szögtartományba eső része egyszersmind a KD körnek is része, így csak azt kell megvizsgálnunk, hogy a KB, KD körök mikor fedik le az ABD háromszöget. a>1 esetén a KB kör az AB szakaszból egységnyi hosszúságú részt vág le, a KD körből az AB egyenesre eső húr hossza pedig 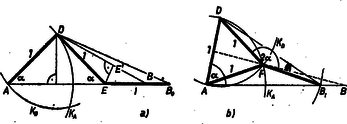2cosα.
 

 

2. ábra
 

Ha e két kör lefedi az AB szakaszt, e részek összege nem kisebb az AB szakasz hosszánál (2a ábra):
a≤2cosα+1.(2)
Ez a≤1 esetén is teljesül, tehát 0<α≤60∘ mellett a fedés szükséges feltétele. Feltételünk úgy is fogalmazható, hogy az ABD háromszög része legyen annak az AB0D háromszögnek, melyben AB0=2cosα+1. Messe KD az AB egyenest E-ben, akkor AD=DE=EB0=1.
Megmutatjuk, hogy (2) elégséges feltétel. Valóban, KD lefedi az AED háromszöget, így ha B az AE szakaszon van, KD maga lefedi az ABD háromszöget. Ha B az EB0 szakaszon van, KB lefedi E-t EB≤1 miatt. Legyen E vetülete BD-n E', akkor az EBE' háromszöget a KB kör, az EE'D háromszöget a KD kör fedi le, hiszen pl. az EBE' háromszögben a B-től legtávolabbi pont az E csúcs, és KB azt is lefedi.
Ha 60∘≤α≤90∘, legyen az AD egyenes B-t tartalmazó oldalán F az a pont, melyre AF=DF=1. Messe az F körüli egységsugarú KF kör az AB egyenest B1-ben. Az AB1F egyenlő szárú háromszögben B1AF∢=α-60∘, ezért (2b ábra)
AB1=2cos(α-60∘)=cosα+3sinα.
Így pedig a feladat állításában szereplő (1) feltétel esetünkben ekvivalens azzal, hogy B az AB1 szakaszon legyen, vagyis az AB1D háromszög tartalmazza az ABD háromszöget. Megmutatjuk, hogy 60∘≤α≤90∘ mellett ez szükséges és elégséges feltétele annak, hogy a KA, KB, KD körök lefedjék az ABD háromszöget.
Feltételünk elégséges, hiszen ha B az AB1 szakaszon van, az F pontot mindhárom kör lefedi, és ebből a fentiekhez hasonlóan látható be, hogy a KA és KB körök együtt lefedik az AFB háromszöget, KB és KD együtt a BFD háromszöget, KA és KD pedig együtt az AFD háromszöget fedik le. (Természetesen nem okoz zavart, ha F nincs is benne az ABD háromszögben.)
Fordítva, ha B az AB1 szakasz B1-en túli meghosszabbításán van, az FB egyenes a KA, KD körök belsejében levő AD szakaszt annak belsejében metszi, így F az ABD háromszög belsejében van, és a KA, KD körök az FB szakasznak csak az F végpontját fedik le. B viszont a KF körön kívül van, tehát FB>1, így az FB szakaszt nem fedheti le teljes egészében a KB kör. Eszerint feltételünk szükséges is.
Összefoglalva az eddigieket: ha az ABD háromszög tetszőleges, akkor 0< <α≤60∘ esetén (2), 60∘≤α≤90∘ esetén (1) a szükséges és elégséges feltétele annak, hogy a KA, KB, KC, KD körök lefedjék az ABCD paralelogrammát.
 

II. Utolsó lépésként megmutatjuk, hogy ha 0<α≤60∘, és az ABD háromszög hegyesszögű, akkor (1) is, (2) is mindig teljesül. Valóban, a 2a ábrán ADB0∢=180∘-3α/2, a 2b ábrán ADB1∢=150∘-α, tehát 0<α≤60∘ mellett mindkettő tompaszög; ha tehát az ABD háromszögben D-nél hegyesszög van, az AB0D, ill. az AB1D háromszög tartalmazza az ABD háromszöget.
Ha tehát 0<α≤60∘, és az ABD háromszög hegyesszögű, köreink mindig fedik a paralelogrammát, és az (1) feltétel is mindig teljesül, így hegyesszögű ABD háromszög esetén (1) az egész 0<α<90∘ intervallumban szükséges és elégséges feltétele a fedésnek.
 

Megjegyzés. Hasonló módon látható, hogy ha az ADB∢ tompaszög, és 60∘<α≤90∘, akkor a körök sosem fedik az ABCD paralelogrammát.