Feladat:	B.5016	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Lovas Márton
Füzet:	2020/március, 157 - 158. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Síkgeometriai bizonyítások, Alakzatok hasonlósága
Hivatkozás(ok):	Feladatok: 2019/március: B.5016

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Legyen $AB=a$ és $CD=c$. A $C{E}_2{F}_1$ és a $CAB$ háromszögek hasonlóak, mivel $ACB\sphericalangle =E_{2}C{F}_1\sphericalangle$, valamint $\begin{array}{c}{\displaystyle \frac{C{E}_2}{CA}=\frac{C{E}_2}{C{E}_2+E_{2}A}=\frac{1}{\frac{C{E}_2+E_{2}A}{C{E}_2}}=\frac{1}{1+\frac{E_{2}A}{C{E}_2}}=\frac{1}{1+\frac{a}{c}}=\frac{1}{\frac{c+a}{c}}=\frac{c}{c+a}}\end{array}$ és $\begin{array}{c}{\displaystyle \frac{C{F}_1}{CB}=\frac{C{F}_1}{C{F}_1+F_{1}B}=\frac{1}{\frac{C{F}_1+F_{1}B}{C{F}_1}}=\frac{1}{1+\frac{F_{1}B}{C{F}_1}}=\frac{1}{1+\frac{a}{c}}=\frac{1}{\frac{c+a}{c}}=\frac{c}{c+a}\mathrm{.}}\end{array}$ Így $\frac{E_2{F}_1}{AB}=\frac{C{E}_2}{CA}=\frac{c}{c+a}$, tehát $E_2{F}_1=\frac{c}{c+a}\cdot a=\frac{ac}{c+a}$. A fentiekhez hasonlóan $\frac{C{E}_2}{CA}=\frac{C{F}_1}{CB}=\frac{D{E}_1}{DA}=\frac{D{F}_2}{DB}$. Ezt és a megfelelő szögek egyenlőségét felhasználva: ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle C{E}_2{F}_1\Delta }& {\displaystyle \sim CAB\Delta \mathrm{,}}\hfill & \text{(<mn>1</mn>)}\\ \hfill {\displaystyle E_{1}A{E}_2\Delta }& {\displaystyle \sim DAC\Delta \mathrm{,}}\hfill & \text{(<mn>2</mn>)}\\ \hfill {\displaystyle F_{2}B{F}_1\Delta }& {\displaystyle \sim DBC\Delta \mathrm{,}}\hfill & \text{(<mn>3</mn>)}\\ \hfill {\displaystyle D{E}_1{F}_2\Delta }& {\displaystyle \sim DAB\Delta \mathrm{.}}\hfill & \text{(<mn>4</mn>)}\end{array}}$ (1) és (4) esetében a hasonlósági arány $\frac{c}{c+a}$, így $E_1{F}_2=E_2{F}_1=a\cdot \frac{c}{c+a}=\frac{ac}{c+a}$. (2) és (3) esetében a hasonlósági arány $\frac{a}{c+a}$, így $E_1{E}_2=F_1{F}_2=c\cdot \frac{a}{c+a}=\frac{ac}{c+a}$. Tehát $E_1{E}_2{F}_1{F}_2$ rombusz, ezért az átlói merőlegesek egymásra (1. ábra). 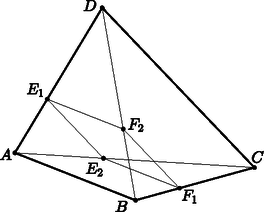    1. ábra    Lovas Márton (Budapest, Békásmegyeri Veres Péter Gimn., 8. évf.)     II. megoldás. Célunk belátni, hogy az $\overrightarrow{E_1{F}_1}$ és $\overrightarrow{E_2{F}_2}$ vektorok merőlegesek egymásra, ami pontosan akkor teljesül, ha a skaláris szorzatuk 0. Jelölje a $\overrightarrow{DA}$, $\overrightarrow{DC}$, $\overrightarrow{AB}$ vektorokat rendre $\text{a}$, $\text{c}$, illetve $\text{b}$, hosszukat a megfelelő kisbetű; legyen továbbá $\frac{b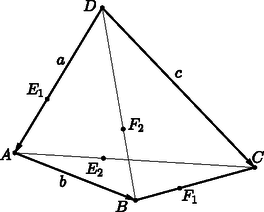}{b+c}=\beta$ (2. ábra).     2. ábra   Ekkor $\begin{array}{c}{\displaystyle \overrightarrow{CB}=\overrightarrow{DB}-\overrightarrow{DC}=\left(\text{a}+\text{b}\right)-\text{c}\mathrm{,}\overrightarrow{BD}=-\text{a}-\text{b}\mathrm{,}\overrightarrow{AC}=-\text{a}+\text{c}\mathrm{,}}\end{array}$   ezért   ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \overrightarrow{A{E}_2}}& {\displaystyle =\beta \overrightarrow{AC}=-\beta \text{a}+\beta \text{c}\mathrm{,}}\hfill \\ \hfill {\displaystyle \overrightarrow{A{F}_2}}& {\displaystyle =\overrightarrow{AB}+\overrightarrow{B{F}_2}=\text{b}+\beta \overrightarrow{BD}=\text{b}+\beta \left(-\text{b}-\text{a}\right)=-\beta \text{a}+\left(1-\beta \right)\text{b}\mathrm{,}}\hfill \end{array}}$ így $\overrightarrow{E_2{F}_2}=\overrightarrow{A{F}_2}-\overrightarrow{A{E}_2}=\left(-\beta \text{a}+\left(1-\beta \right)\text{b}\right)-\left(-\beta \text{a}+\beta \text{c}\right)=\left(1-\beta \right)\text{b}-\beta \text{c}$. Hasonlóan   ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \overrightarrow{B{F}_1}}& {\displaystyle =\beta \overrightarrow{BC}=\beta \left(\overrightarrow{DC}-\overrightarrow{DB}\right)=\beta \text{c}-\beta \left(\text{a}+\text{b}\right)=-\beta \text{a}-\beta \text{b}+\beta \text{c}\mathrm{,}}\hfill \\ \hfill {\displaystyle \overrightarrow{B{E}_1}}& {\displaystyle =\overrightarrow{BA}+\overrightarrow{A{E}_1}=-\text{b}-\beta \text{a}\mathrm{,}}\hfill \end{array}}$ ezért $\overrightarrow{E_1{F}_1}=\overrightarrow{B{F}_1}-\overrightarrow{B{E}_1}=\left(1-\beta \right)\text{b}+\beta \text{c}$. Felírva $\overrightarrow{E_1{F}_1}$ és $\overrightarrow{E_2{F}_2}$ skaláris szorzatát: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \overrightarrow{E_1{F}_1}\cdot \overrightarrow{E_2{F}_2}}& {\displaystyle =\left(\left(1-\beta \right)\text{b}+\beta \text{c}\right)\left(\left(1-\beta \right)\text{b}-\beta \text{c}\right)={\left(1-\beta \right)}^2{b}^2-{\beta }^2{c}^2=}\hfill \\ \hfill {\displaystyle }& {\displaystyle ={\left(\frac{b+c-b}{b+c}\right)}^2{b}^2-{\left(\frac{b}{b+c}\right)}^2{c}^2=\frac{c^2{b}^2}{{\left(b+c\right)}^2}-\frac{b^2{c}^2}{{\left(b+c\right)}^2}=0.}\hfill \end{array}}$ Tehát a két vektor skaláris szorzata 0, vagyis merőlegesek egymásra.