Kezdőlap


Feladat:	B.5013	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Asztalos Ádám , Beke Csongor , Csaplár Viktor , Kovács Tamás , Nagy Nándor , Rares Polenciuc , Tiderenczl Dániel , Várkonyi Zsombor , Weisz Máté
Füzet:	2020/március, 155 - 156. oldal		PDF \| MathML
Témakör(ök):	Feladat, Síkgeometriai bizonyítások, Háromszög nevezetes körei, Síkgeometriai számítások trigonometriával
Hivatkozás(ok):	Feladatok: 2019/február: B.5013

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az $A$ -val szemközti hozzáírt kör és a beírt kör érintsék a $B C$ oldalt rendre az $E$ és $F$ pontokban. Legyen $B_{1} B C ∢ = α$ , $E B_{1} B_{2} ∢ = β$ . A $B_{3} E B_{2} ∢$ a hozzáírt körön a $B_{2} E$ ívhez tartozó érintőszárú kerületi szög, így $B_{3} E B_{2} ∢ = E B_{1} B_{2} ∢ = β$ , és hasonlóan $E B_{2} B_{3} ∢ = β$ . Így $B B_{3} B_{2} ∢ = 2 β$ , ezért $B B_{2} B_{3} ∢ = 180^{\circ} - α - 2 β$ . Innen $E B_{2} B_{1} ∢ = 180^{\circ} - B B_{2} B_{3} ∢ - E B_{2} B_{3} ∢$ miatt $E B_{2} B_{1} ∢ = α + β$ adódik. Ez a hozzáírt körön a rövidebb $E B_{1}$ ívhez tartozó kerületi szög, ami egyenlő az ehhez az ívhez tartozó érintőszárú kerületi szögekkel, tehát $C E B_{1} ∢ = C B_{1} E ∢ = α + β$ , és így $B_{1} C E ∢ = 180^{\circ} - 2 α - 2 β$ . Könnyű látni azt is, hogy 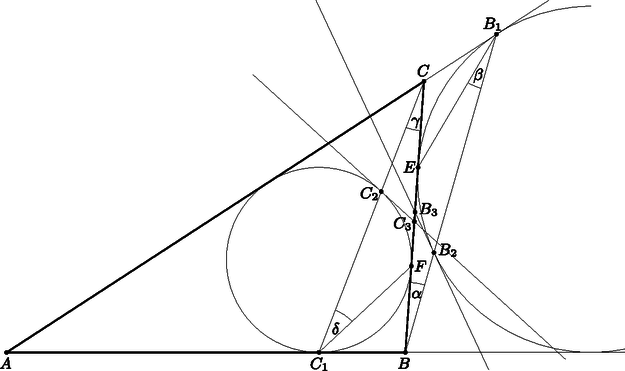$B B_{1} C ∢ = E B_{1} B_{2} ∢ + E B_{1} C ∢ = β + (α + β) = α + 2 β$ .

Írjuk fel ezután a szinusztételt a

B B_{2} B_{3}

és a

B C B_{1}

háromszögekre:

\begin{matrix} \frac{B B_{3}}{B_{3} E} & = \frac{B B_{3}}{B_{3} B_{2}} = \frac{sin (180^{\circ} - α - 2 β)}{sin α} = \frac{sin (α + 2 β)}{sin α}, \\ \frac{B C}{C B_{1}} & = \frac{sin (α + 2 β)}{sin α}; \end{matrix}

ezekből

\frac{B B_{3}}{B_{3} E} = \frac{B C}{C B_{1}}

, így

\frac{B E}{B_{3} E} = \frac{B B_{3} + B_{3} E}{B_{3} E} = \frac{B B_{3}}{B_{3} E} + 1 = \frac{B C}{C B_{1}} + 1

, ezért (a szokásos jelölésekkel)

\begin{matrix} B_{2} B_{3} = B_{3} E = \frac{B E}{\frac{B C}{C B_{1}} + 1} = \frac{s - c}{\frac{a}{s - b} + 1} . \end{matrix}

Hasonlóan, legyen

C_{2} C C_{3} ∢ = γ

C C_{1} F ∢ = δ

. Ekkor a rövidebbik

C_{2} F

ívhez tartozó érintőszárú kerületi szögekként

C_{3} C_{2} F ∢ = C_{3} F C_{2} ∢ = δ

, ezért

C_{2} C_{3} C ∢ = 2 δ

, így

C C_{2} C_{3} ∢ = 180^{\circ} - (γ + 2 δ)

\begin{matrix} C_{1} C_{2} F ∢ & = 180^{\circ} - C C_{2} F ∢ = 180^{\circ} - (C C_{2} C_{3} ∢ + δ) = \\ = 180^{\circ} - (180^{\circ} - (γ + 2 δ) + δ) = γ + δ . \end{matrix}

Innen

C_{2} F C_{1} ∢ = 180^{\circ} - (γ + 2 δ)

B C_{1} F ∢ = B F C_{1} ∢ = γ + δ

, tehát

B C_{1} C ∢ = B C_{1} F ∢ + δ = γ + 2 δ

.
Írjuk fel a szinusztételt, ezúttal a

C C_{2} C_{3}

és a

C C_{1} B

háromszögekre:

\begin{matrix} \frac{C C_{3}}{C_{2} C_{3}} = \frac{sin (γ + 2 δ)}{sin γ}, \frac{B C}{B C_{1}} = \frac{sin (γ + 2 δ)}{sin γ}, \end{matrix}

ezért

\frac{C C_{3}}{C_{3} F} = \frac{C C_{3}}{C_{2} C_{3}} = \frac{B C}{B C_{1}}

\frac{C F}{C_{3} F} = \frac{C C_{3} + C_{3} F}{C_{3} F} = \frac{C C_{3}}{C_{3} F} + 1 = \frac{B C}{B C_{1}} + 1

, így

\begin{matrix} C_{2} C_{3} = C_{3} F = \frac{C F}{\frac{B C}{B C_{1}} + 1} . \end{matrix}

Tehát

\begin{matrix} C_{2} C_{3} = \frac{C F}{\frac{B C}{B C_{1}} + 1} = \frac{s - c}{\frac{a}{s - b} + 1} = B_{2} B_{3} . \end{matrix}

Weisz Máté (Szegedi Radnóti Miklós Kísérleti Gimn., 11. évf.)