| Feladat: | 2019. évi Kürschák matematikaverseny 1. feladata | Korcsoport: 18- | Nehézségi fok: nehéz |
| Megoldó(k): | Pach Péter Pál | ||
| Füzet: | 2020/február, 67 - 68. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Kürschák József (korábban Eötvös Loránd), Síkgeometriai bizonyítások | ||
| Hivatkozás(ok): | Feladatok: 2020/február: 2019. évi Kürschák matematikaverseny 1. feladata | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Először megmutatjuk, hogy a pont az , a pedig az szakasznak belső pontja. Legyen az csúcsnak a magasságra vonatkozó tükörképe. Az feltétel miatt , ezért az pont a szakasznak belső pontja. A szakasz a háromszög belsejében halad, és ennek belső pontja, tehát a háromszög belsejébe esik. 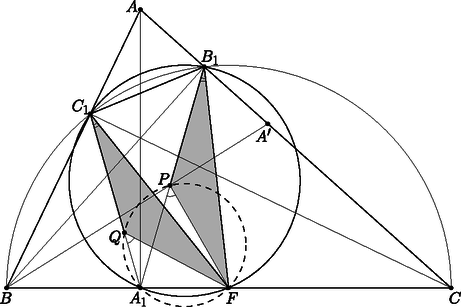 Legyen felezőpontja ; az és szakaszok a oldal Thalész-körének sugarai, ezért . Szintén jól ismert, hogy az , , pontok egy körön, a háromszög Feuerbach-körén vannak. Vegyük észre, hogy az és háromszögek egybevágók, mert , , és az ívhez tartozó kerületi szögek a Feuerbach-körön. Tehát |