Kezdőlap


Feladat:	B.4989	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Baski Bence , Bursics András , Dobák Dániel , Füredi Erik Benjámin , Geretovszky Anna , Győrffy Johanna , Györffi Ádám György , Hegedűs Dániel , Kirschner Bernadett , Nagy Nándor , Rares Polenciuc , Soós Máté , Szabó Dávid , Szabó Kornél , Terjék András , Török Mátyás , Velich Nóra , Weisz Máté , Zsigri Bálint
Füzet:	2019/szeptember, 348 - 350. oldal		PDF \| MathML
Témakör(ök):	Feladat, Síkgeometriai bizonyítások, Háromszögek geometriája, Súlypont
Hivatkozás(ok):	Feladatok: 2018/november: B.4989

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Tükrözzük az $A$ csúcsot a $D$ pontra, a tükörképet jelölje $A'$ . Mivel $A A'$ és $B C$ a $D$ pontban felezik egymást, ezért 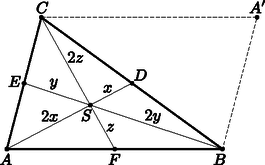$A B A' C$ paralelogramma.

A paralelogramma-tételt felírva kapjuk, hogy

\begin{matrix} A A'^{2} + B C^{2} = A B^{2} + B A'^{2} + A' C^{2} + C A'^{2} . \end{matrix}

A háromszög oldalait és súlyvonalait a szokásos módon jelölve és kihasználva, hogy

A B = C A'

és

B A' = A C

kapjuk, hogy

\begin{matrix} {(2 s_{a})}^{2} + a^{2} = c^{2} + b^{2} + c^{2} + b^{2}, \\ 4 s_{a}^{2} = 2 b^{2} + 2 c^{2} - a^{2}, \\ s_{a} = \sqrt[]{\frac{2 b^{2} + 2 c^{2} - a^{2}}{2}} . \end{matrix}

Hasonló a képlet

s_{b}

-re és

s_{c}

-re. A képletekből látható, hogy ha egy oldal legalább akkora, mint egy másik, akkor a hozzá tartozó súlyvonal legfeljebb akkora, mint a másikhoz tartozó. Az is következik, hogy ha az

a

-hoz és

b

-hez tartozó súlyvonal hossza egyenlő, akkor

a = b

, hiszen felírva a képletet a két súlyvonalra, és egyenlővé téve őket, majd négyzetre emelve és rendezve azt kapjuk, hogy

a^{2} = b^{2}

.
Legyen az

a

-hoz tartozó súlyvonal hossza

3 x

, a

b

-hez tartozó

3 y

, a

c

-hez tartozó pedig

3 z

. A súlypont harmadolja a súlyvonal háromszögbe eső szakaszát, tehát az egyes háromszögek kerületeit fel tudjuk írni ezeknek a szakaszoknak a segítségével.
A szimmetria miatt feltehetjük, hogy

a

-nál nincs hosszabb oldal. Ezután két esetet különböztetünk meg:

b \geq c

és

b \leq c

.
Kezdjük az első esettel. Ekkor tehát

a \geq b \geq c

. Ennek alapján

x \leq y \leq z

. Tudjuk, hogy az

A F S

és

C E S

háromszögek kerülete egyenlő. Az

A F S

háromszög kerülete

\frac{c}{2} + z + 2 x

, a

C E S

háromszögé pedig

\frac{b}{2} + y + 2 z

. Tudjuk továbbá, hogy

\begin{matrix} \frac{c}{2} \leq \frac{b}{2}, z \leq z, x \leq y, x \leq z . \end{matrix}

Ezt a négy egyenlőtlenséget összeadva azt kapjuk, hogy

A F S

kerülete legfeljebb akkora, mint

C E S

kerülete. Viszont a feladat szövege szerint ezek egyenlőek, ami pedig csak akkor lehet, ha minden egyenlőtlenségben az egyenlőség esete teljesül. Tehát

\frac{c}{2} = \frac{b}{2}

, vagyis

c = b

; és

x = y

, vagyis a második bekezdés értelmében ekkor

a = b

. Tehát

a = b = c

, a háromszög szabályos.
A másik eset nagyon hasonló. Ekkor

a \geq c \geq b

, emiatt

x \leq z \leq y

. Ebben az esetben a feladat szövege alapján az

A F S

háromszög kerülete

(\frac{c}{2} + 2 x + z)

megegyezik a

B D S

háromszög kerületével

(\frac{a}{2} + x + 2 y)

. Felírva, majd összeadva az

\begin{matrix} \frac{a}{2} \geq \frac{c}{2}, x \geq x, y \geq x, y \geq z \end{matrix}

egyenlőtlenségeket, azt kapjuk, hogy

B D S

kerülete legalább akkora, mint

A F S

kerülete, és egyenlőség csak akkor lehet, ha minden egyenlőtlenségnél az egyenlőség esete áll fenn. Ekkor pedig

a = c

; és

y = z

, amiből következik, hogy

b = c

. Tehát

a = b = c

, vagyis a háromszög szabályos.
Mindkét esetben azt kaptuk, hogy ha a feltétel igaz, akkor a háromszög biztosan szabályos.

Dobák Dániel (Budapesti Fazekas M. Gyak. Ált. Isk. és Gimn. , 12. évf.)