Kezdőlap


Feladat:	5124. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Máth Benedek , Tiefenbach Flórián
Füzet:	2019/szeptember, 374 - 376. oldal		PDF \| MathML
Témakör(ök):	Feladat, Erőrendszer eredője
Hivatkozás(ok):	Feladatok: 2019/április: 5124. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$a)$ Legyen a hengerek közötti sugárirányú tartóerő (nyomóerő) $T_{2}$ , a közöttük fellépő, érintő irányú súrlódási erő $F_{2} = T_{2} μ_{2}$ ; az alsó testek és a talaj között fellépő tartóerő $T_{1}$ , a súrlódási erő pedig $F_{1} = T_{1} μ_{1}$ . (Itt $μ_{1}$ és $μ_{2}$ az alsó és a felső érintkezési pontokhoz tartozó kritikus súrlódási együtthatókat jelöli, vagyis azt az értéket, amelynél még éppen nem csúszik meg egyik henger sem.)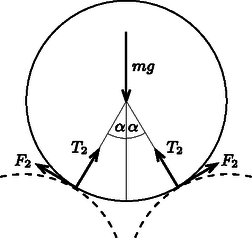
A felső testre ható erőket az 1. ábra, az egyik alsó testre ható erőket a 2. ábra mutatja. A hengerek tengelyének merőleges metszete egy szabályos háromszöget alkot, ezért $α = 30^{\circ}$ .

1. ábra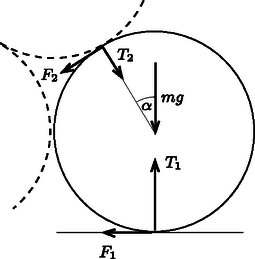

2. ábra

Megjegyzés. Feltételezzük, hogy két alsó henger éppen nem érintkezik egymással, így nem fejtenek ki egymásra erőt. Elvben elképzelhető, hogy ez nem teljesül, mert a két alsó henger is egymásnak szorul. Belátható, hogy ebben az esetben mindkét súrlódási együtthatónak nagyobbnak kellene lennie, mint az összeszorulás-mentes elrendezésben. Mivel ebben a feladatban a legkisebb (az egyensúlyhoz még éppen elegendő) súrlódási együtthatókat keressük, az összeszorulás lehetőségét a továbbiakban figyelmen kívül hagyhatjuk.

Felírhatjuk, hogy a felső és az alsó testre ható erők függőleges komponensei (külön-külön) egyensúlyban vannak, továbbá az alsó testre ható vízszintes erőkomponensek és a forgatónyomatékok eredője is nulla:

\begin{matrix} m g & = 2 T_{2} (cos α + μ_{2} sin α), & (1) \\ m g & = T_{1} - T_{2} (cos α + μ_{2} sin α), & (2) \\ μ_{1} T_{1} & = T_{2} (sin α - μ_{2} cos α), & (3) \\ μ_{1} T_{1} & = μ_{2} T_{2} . & (4) \end{matrix}

Ezekből (algebrai átalakítások után) a

\begin{matrix} μ_{2} = \frac{sin α}{1 + cos α} = \frac{sin (30^{\circ})}{1 + cos (30^{\circ})} = 2 - \sqrt[]{3} \approx 0, 27, \end{matrix}

T_{1} = 3 T_{2}

, valamint a

\begin{matrix} μ_{1} = \frac{T_{2}}{T_{1}} (sin α - μ_{2} cos α) = \frac{2 - \sqrt[]{3}}{3} \approx 0, 09 \end{matrix}

eredményt kapjuk.
A hengeres testek között legalább 0,27-nek, az alsó hengerek és az asztal között pedig legalább 0,09-nek kell lennie a súrlódási együtthatónak, hogy a testek egyensúlyban maradhassanak.

b)

A fentiekhez hasonlóan tárgyalható a tömör gömbök egyensúlyának feltétele is. A gömbök középpontjai szabályos tetraédert alkotnak, ezért a felső és az alsó gömbök között fellépő erők függőlegessel bezárt szöge

α = {35, 3}^{\circ}

.
A felső testre három tartóerő és három súrlódási erő hat, ezért az első egyenlet kissé módosul:

\begin{matrix} m g = 3 T_{2} (cos α + μ_{2} sin α) . \end{matrix}

(1')

A többi egyenlet nem változik (az

α

változásán kívül):

\begin{matrix} m g & = T_{1} - T_{2} (cos α + μ_{2} sin α), & (2') \\ μ_{1} T_{1} & = T_{2} (sin α - μ_{2} cos α), & (3') \\ μ_{1} T_{1} & = μ_{2} T_{2} . & (4') \end{matrix}

Ezekből következik, hogy

T_{1} = 4 T_{2}

, továbbá

\begin{matrix} μ_{2} & = \frac{sin α}{1 + cos α} = \frac{sin ({35, 3}^{\circ})}{1 + cos ({35, 3}^{\circ})} = 0, 32, \\ μ_{1} & = \frac{sin {35, 3}^{\circ} - 0, 32 cos {35, 3}^{\circ}}{4} = 0, 08. \end{matrix}

Négy egyforma, homogén gömb esetében a gömbök között legalább 0,32-nek, a gömbök és az asztal között pedig legalább 0,08-nak kell lennie a súrlódási együthatónak, hogy a rendszer egyensúlyban maradhasson.

Tiefenbeck Flórián (Budapest, Fazekas M. Gyak. Ált. Isk. és Gimn., 11. évf.)
dolgozata alapján

Megjegyzés. Vegyük észre, hogy a három henger esetében a fellépő erők egy síkban hatnak! Ez azt jelenti, hogy az egyensúly feltétele független attól, hogy hengerek vagy gömbök állnak az asztalon. (A gömbök esetében is egy síkban hatnak az erők, és ebben a síkban a hengerek és a gömbök metszete megegyezik.) Ezt felhasználva a feladatban szereplő két konkrét problémát általánosíthatjuk. Legyen

n

darab (

1 < n \leq 5

) egyforma gömb az asztalon olyan módon elhelyezve, hogy mindegyik két másikkal ér össze, és a középpontjaik egy

n

oldalú szabályos sokszöget alkotnak (kivéve az

n = 2

esetet, amelynél a középpontok egy egyenesen helyezkednek el). Fontos, hogy bár összeérnek az asztalon lévő gömbök, de nem fejtenek ki egymásra erőt.

A megoldás menete hasonló a fentebb leírtakkal, és a súrlódási együtthatókra adódó eredmény:

\begin{matrix} μ_{test-test} & \geq \frac{1}{2 sin (π / n) + \sqrt[]{4 sin^{2} (π / n) - 1}}, \\ μ_{test-asztal} & = \frac{1}{n + 1} μ_{test-test} . \end{matrix}

Ezekből

n = 2

esetén megkapjuk az

a)

kérdésnek,

n = 3

esetén pedig a

b)

kérdésnek megfelelő eredményt.

Máth Benedek (Budapest, Fazekas M. Gyak. Ált. Isk. és Gimn., 12. évf.)