Kezdőlap


Feladat:	B.4987	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bares Polenciuc , Baski Bence , Beke Csongor , Csaplár Viktor , Csertán András , Dobák Dániel , Fekete Richárd , Fülőp Anna Tácia , Hámori Janka , Hegedűs Dániel , Jánosik Áron , Kerekes Anna , Kovács Tamás , Mátravölgyi Bence , Nguyen Bich Diep , Snehansu Bhowmick , Szabó Dávid , Tálos Zoltán , Tiderenczl Dániel , Tóth Balázs , Velich Nóra , Weisz Máté , Zsigri Bálint
Füzet:	2019/május, 286. oldal		PDF \| MathML
Témakör(ök):	Feladat, A háromszögek nevezetes pontjai, Síkgeometriai bizonyítások, Húrnégyszögek
Hivatkozás(ok):	Feladatok: 2018/november: B.4987

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$a)$ Legyenek $I$ és $H$ rendre az $M$ pont tükörképei az $F$ és $D$ pontok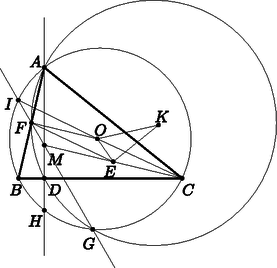ra.

Közismert, hogy ekkor

I

és

H

rajta vannak az

A B C

háromszög köré írt körön. A húrtétel szerint

I M \cdot M G = H M \cdot M A

(az

M

pontnak az

A B C

háromszög körülírt körére vonatkozó hatványa), ezért

\begin{matrix} 2 F M \cdot M G = 2 D M \cdot M A, \end{matrix}

vagyis

F M \cdot M G = D M \cdot M A

. Ebből a húrtétel megfordítása miatt következik, hogy

A F D G

húrnégyszög.

b)

F

-re középpontosan tükrözve az

A M F

háromszöget a

B I F

háromszöget kapjuk, így

D A B ∢ = M A F ∢ = I B F ∢ = I B A ∢

. Így

I B C ∢ = I B A ∢ + A B C ∢ = D A B ∢ + A B D = 90^{\circ}

. Tehát

I C

A I B H C G

kör átmérője a Thalész-tétel megfordítása miatt, vagyis

O

felezi

I C

-t. Ekkor a Thalész-tétel szerint

I G C ∢ = 90^{\circ}

, ezért

M G C ∢ = 90^{\circ}

, és ezzel ‐ ismét a Thalesz-tétel megfordítását alkalmazva ‐ kapjuk, hogy

G

rajta van az

M C

átmérőjű körön, melynek középpontja

E

. Így

E M = E G = E C

. AZ

O E F

M I C

háromszög középvonal-háromszöge, ugyanis

O

felezi az

I C

E

M C

F

pedig az

M I

szakaszt. Ezért

O E ∥ I M ∥ F G

, továbbá

O F = E M = E G

. Tehát

O E G F

trapéz, melynek szárai egyenlő hosszúak, vagyis húrtrapéz. Így

F G

felezőmerőlegese megegyezik

O E

felezőmerőlegesével, hiszen ez a trapéz szimmetriatengelye. Mivel

K

A F D G

kör középpontja, rajta kell lennie

F G

felezőmerőlegesén, ekkor viszont rajta van

O E

felezőmerőlegesén is. Ez pedig ekvivalens azzal, hogy

E K = O K

Weisz Máté (Szegedi Radnóti Miklós Kísérleti Gimn., 11. évf.)