Kezdőlap


Feladat:	B.4977	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Bokor Endre , Bukva Dávid , Csertán András , Zsigri Bálint
Füzet:	2019/március, 153 - 157. oldal		PDF \| MathML
Témakör(ök):	Feladat, Síkgeometriai bizonyítások, Magasságvonal, Beírt kör
Hivatkozás(ok):	Feladatok: 2018/október: B.4977

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen a háromszög három csúcsa

A

B

és

C

, melyek közül

C

a derékszögű csúcs, és jelölje a

B

-nél lévő szöget

β

, az

A

-nál lévő szög ekkor

α = 90^{\circ} - β

. Legyenek beírt kör érintési pontjai az

A B

A C

B C

oldalakon

T

E

D

, a

T D E

háromszög magasságpontja

M

, és a beírt kör középpontja

O

. Ekkor

O E C D

egy négyzet. Legyen

E_{1}

és

D_{1}

E T D

háromszög

E

-ből, illetve

D

-ből induló magasságának talppontja.

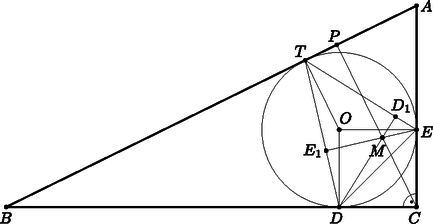1. ábra

Végül legyen

P

A B C

háromszög

C

-hez tartozó magasságtalppontja,

M_{D}

P C

és

D M

egyenes metszéspontja,

M_{E}

pedig a

P C

és

E M

egyenes metszéspontja.
Végezzünk szögszámítást.

\begin{matrix} E D M ∢ = E D D_{1} ∢ = 90^{\circ} - D_{1} E D ∢ = 90^{\circ} - T E D ∢ . \end{matrix}

A középponti és kerületi szögek tételéből

\begin{matrix} E D M ∢ = 90^{\circ} - \frac{T O D ∢}{2} . \end{matrix}

Mivel

O D B ∢ = O T B ∢ = 90^{\circ}

, ezért

O T B D

húrnégyszög, így

\begin{matrix} E D M_{D} ∢ = E D M ∢ = 90^{\circ} - \frac{180^{\circ} - β}{2} = \frac{β}{2} . \end{matrix}

Hasonló módon

\begin{matrix} D E M ∢ = D E E_{1} ∢ = 90^{\circ} - E D E_{1} ∢ = 90^{\circ} - E D T ∢ = 90^{\circ} - \frac{E O T ∢}{2}, \end{matrix}

O E A ∢ = O T A ∢ = 90^{\circ}

O T A E

húrnégyszög, és

\begin{matrix} D E M_{E} ∢ = D E M ∢ = 90^{\circ} - \frac{180^{\circ} - (90^{\circ} - β)}{2} = 45^{\circ} - \frac{β}{2} . \end{matrix}

Ismert továbbá, hogy

A C P ∢ = β

P C B ∢ = 90^{\circ} - β

, és

C A P ∢ = 90^{\circ} - β

. Ezekből következik, hogy

E C M_{E} ∢ = β

és

D C M_{D} ∢ = 90^{\circ} - β

.
Mivel

O E C D

négyzet, így

C E D ∢ = C D E ∢ = 45^{\circ}

, vagyis

\begin{matrix} C E M_{E} ∢ & = C E D ∢ + D E M_{E} ∢ = 90^{\circ} - \frac{β}{2}, és \\ C D M_{D} ∢ & = C D E ∢ + E D M_{D} ∢ = 45^{\circ} + \frac{β}{2} . \end{matrix}

Mivel

E C M_{E} ∢ = A C P ∢ = β

és

C E M_{E} ∢ = 90^{\circ} - β / 2

, ezért

\begin{matrix} E M_{E} C ∢ = 180^{\circ} - β - (90^{\circ} - \frac{β}{2}) = 90^{\circ} - \frac{β}{2}, \end{matrix}

vagyis az

E C M_{E}

háromszög egyenlő szárú,

E C = C M_{E}

.
Mivel

D C M_{D} ∢ = P C B ∢ = 90^{\circ} - β

és

C D M_{D} ∢ = 45^{\circ} + β / 2

, ezért

\begin{matrix} D M_{D} C ∢ = 180^{\circ} - (90^{\circ} - β) - (45^{\circ} + \frac{β}{2}) = 45^{\circ} + \frac{β}{2}, \end{matrix}

vagyis

D C M_{D}

háromszög egyenlő szárú,

D C = C M_{D}

.
Mivel

O E C D

négyzet, így

E C = D C

, vagyis

C M_{E} = C M_{D}

, tehát

M_{E} \equiv \equiv M_{D} \equiv M

, tehát

M

rajta van a derékszögű csúcshoz tartozó magasságvonalon.
Az egyetlen kritikus pont a bizonyításban annak feltételezése, hogy a

T E D

háromszög hegyesszögű (ebből következik, hogy

M

a háromszög belsejében van és az ábrán megfelelően állnak a szögek). A fentiek alapján

\begin{matrix} T E D ∢ = \frac{T O D ∢}{2} = \frac{180^{\circ} - β}{2} = 90^{\circ} - \frac{β}{2} . \end{matrix}

Mivel

β

0^{\circ}

és

90^{\circ}

közt van, így ez hegyesszög.

\begin{matrix} E D T ∢ = \frac{E O T ∢}{2} = \frac{180^{\circ} - (90^{\circ} - β)}{2} = 45^{\circ} + \frac{β}{2} . \end{matrix}

Mivel

β

0^{\circ}

és

90^{\circ}

közt van, így ez hegyesszög.

E T D ∢ = 180^{\circ} - T E D ∢ - E D T ∢ = 45^{\circ}

. Ezek alapján a

T E D

háromszög valóban hegyesszögű.

Zsigri Bálint (Budapest XIV. Ker. Szent István Gimn., 12. évf.)

II. megoldás. Helyezzük el a háromszöget a derékszögű koordinátarendszerben a 2. ábrán látható módon. A derékszögű háromszög beírt körének érintési pontjait jelölje

K_{1}

K_{2}

és

K_{3}

. A

K_{1}

-hez és

K_{3}

-hoz tartozó magasságvonalak legyenek

m_{1}

és

m_{3}

, a

c

oldalhoz tartozó pedig

m_{c}

. Felírva ezen magasságvonalak egyenleteit könnyen ellenőrizhetjük, hogy valóban egy pontban metszik-e egymást. Legyen

B A C ∢ = α

A B C ∢ = β

és jelölje

γ

az ábrán berajzolt szöget.

2. ábra

Mivel

m_{3}

és az

A O

szögfelező is merőleges

K_{1} K_{2}

-re, ezért párhuzamosak egymással. Az

O K_{3} C K_{1}

négyszög egy

r

oldalú négyzet, ezért

m_{3}

- r

koordinátánál metszi az

x

tengelyt, így egyenlete

y = tg γ \cdot x + tg γ \cdot r

. Hasonlóan belátható, hogy

m_{1}

párhuzamos

B O

-val és az

y

tengelyt

r

-nél metszi. Az egyenlete

y = tg \frac{β}{2} \cdot x + r

. Az

m_{c}

magasság egyenes merőleges a

c

oldalra és az origón megy keresztül, ezért az egyenletét könnyen megkaphatjuk:

y = - \frac{1}{tg α} \cdot x

.
Az

A O

szögfelező és

m_{3}

párhuzamosságából következik, hogy

γ

\frac{α}{2}

pótszöge. Felhasználva, hogy

\frac{α}{2} = \frac{π}{4} - \frac{β}{2}

, ebből

γ = \frac{π}{4} + \frac{β}{2}

adódik. A félszögek tangensére vonatkozó azonosságot felhasználva

tg \frac{β}{2} = \frac{sin β}{1 + cos β}

, valamint

\begin{matrix} tg (\frac{π}{4} + \frac{β}{2}) = tg (\frac{\frac{π}{2} + β}{2}) = \frac{sin (\frac{π}{2} + β)}{1 + cos (\frac{π}{2} + β)} = \frac{cos β}{1 - sin β} . \end{matrix}

Összegezve:

\begin{matrix} m_{3} egyenlete: & y = tg (\frac{π}{4} + \frac{β}{2}) \cdot x + tg (\frac{π}{4} + \frac{β}{2}) \cdot r = (x + r) \frac{cos β}{1 - sin β}, \\ m_{1} egyenlete: & y = tg \frac{β}{2} \cdot x + r = \frac{sin β}{1 + cos β} \cdot x + r, \\ m_{c} egyenlete: & y = - \frac{1}{tg β} x = - \frac{cos β}{sin β} x . \end{matrix}

m_{1}

és az

m_{3}

egyenes biztosan metszik egymást, méghozzá abban az

x

koordinátájú pontban, amelyre

\begin{matrix} (x + r) \frac{cos β}{1 - sin β} = \frac{sin β}{1 + cos β} x + r . \end{matrix}

Ebből

\begin{matrix} x (\frac{cos β}{1 - sin β} - \frac{sin β}{1 + cos β}) = r (1 - \frac{cos β}{1 - sin β}), \\ x & = r \cdot \frac{1 - \frac{cos β}{1 - sin β}}{\frac{cos β}{1 - sin β} - \frac{sin β}{1 + cos β}} = r \cdot \frac{\frac{1 - sin β - cos β}{1 - sin β}}{\frac{cos β (1 + cos β) - sin β (1 - sin β)}{(1 - sin β) (1 + cos β)}} = \\ = r \cdot \frac{(1 - sin β - cos β) (1 + cos β)}{cos β + cos^{2} β - sin β + sin^{2} β} = \\ = r \cdot \frac{1 - sin β - cos β + cos β - sin β cos β - cos^{2} β}{cos β - sin β + 1} = \\ = \frac{sin β (cos β - sin β + 1)}{cos β - sin β + 1} = - r \cdot sin β . \end{matrix}

Behelyettesítve ezt az

x

értéket

m_{c}

és

m_{3}

egyenletébe:

\begin{matrix} m_{c} : & - \frac{cos β}{sin β} (- sin β \cdot r) = cos β \cdot r, \\ m_{3} : & (- sin β \cdot r + r) \frac{cos β}{1 - sin β} = cos β \cdot r . \end{matrix}

Tehát valóban egy pontban metszik egymást.

Bokor Endre (Budapesti Fazekas M. Gyak. Ált. Isk. és Gimn., 10. évf.)

III. megoldás. Jelölje

K_{1}

K_{2}

és

K_{3}

A B C

háromszögbe írt kör érintési pontjait az oldalakon a 2. ábra szerint, és legyen a

K_{1} K_{2} K_{3}

háromszög magasságpontja

M

.
Külső pontból körhöz húzott érintők hossza egyenlő, tehát

C K_{1} = C K_{3}

. Továbbá az érintési pontba húzott sugár merőleges az érintőre:

O K_{1} C ∢ = O K_{3} C ∢ = 90^{\circ}

. Mindezekből következik, hogy az

O K_{3} C K_{1}

négyszög négyzet.
Legyen

O

az origo, valamint mutasson minden pontba azonos nevű helyvektor

(\vec{O A} = a, ...)

.
Ismert, hogy a háromszög köréírt körének

O

középpontjából a csúcsokba mutató vektorok összege az

O

-ból a magasságpontba mutató vektor. Mivel most

O

K_{1} K_{2} K_{3} ▵

köré írt körének középpontja, ezért

O

-ból e háromszög

M

magasságpontjába az

m = k_{1} + k_{2} + k_{3}

vektor mutat.

O K_{3} C K_{1}

négyzet, ezért egyben paralelogramma is:

c = k_{1} + k_{3}

. Ebből

\vec{C M} = m - c = (k_{1} + k_{3} + k_{2}) - (k_{1} + k_{3}) = k_{2} = \vec{O K_{2}}

.
Tudjuk, hogy

O K_{2} ⊥ A B

, ezért a fentiekből következik, hogy

C M ⊥ A B

, és így

M

rajta van a

C

-ből induló magasságvonalon.

Csertán András (Nagykanizsa, Batthyány L. Gimn., 12. évf.)

IV. megoldás. Az

A B C

háromszögbe írt kör érintési pontjai által meghatározott háromszög legyen

E F G

, és jelölje

I

E L

és

C H

egyenesek metszéspontját (3. ábra).

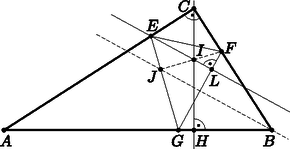3. ábra

Mivel

G F

merőleges a

C B H ∢

szögfelezőjére és merőleges

E L

-re, ezért

E L

párhuzamos a szögfelezővel. Legyen

α = = C A B ∢

és

β = C B A ∢

, ekkor

\begin{matrix} B C H ∢ = α és A C H ∢ = β, H B C_{▵} \sim H C A_{▵} . \end{matrix}

Tehát a

H B C

háromszöget el tudjuk forgatni

H

körül

90

fokkal, majd

H

pont körüli nagyítást alkalmazhatunk úgy, hogy a

B

pont a

C

pontba, a

C

pont pedig az

A

pontba kerüljön. Ekkor a

H A C

háromszöget fogjuk kapni, tehát

E L

merőleges az

A C H ∢

szögfelezőjére (mert 90 fokkal forgattunk és

A H C

és

C H B

hasonlók). Ebből következik, hogy

C E = C I

. Hasonlóan belátható, hogy

F J

merőleges a

B C H ∢

szögfelezőjére. Mivel

C E = C F

(körhöz húzott érintőszakaszok egyenlők), ezért

C F = C I

is teljesül. Emiatt a

B C H ∢

szögfelezője merőleges

F I

-re, vagyis

F

I

és

J

egy egyenesre esnek. Tehát

F J

és

C H

metszéspontja is az

I

pont, azaz

E F G

magasságpontja az

A B C

háromszög

C

-hez tartozó magasságán fekszik.

Bukva Dávid (Budapesti Fazekas M. Gyak. Ált. Isk. és Gimn., 10. évf.)