Feladat:	B.4963	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Kerekes Anna ,  Tubak Dániel
Füzet:	2019/március, 150 - 152. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Síkgeometriai bizonyítások, Háromszög nevezetes körei, Háromszög területe, Algebrai átalakítások
Hivatkozás(ok):	Feladatok: 2018/május: B.4963

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. A legnagyobb sugarú hozzáírt kör a leghosszabb oldalhoz tartozik. Feltehetjük, hogy $a\ge b\ge c$. A háromszögre vonatkozó ismert összefüggések ($s$ a háromszög félkerülete): $\begin{array}{c}{\displaystyle r_a=\frac{T}{s-a}=\frac{2T}{b+c-a}\mathrm{,}R=\frac{abc}{4T}\mathrm{.}}\end{array}$ A bizonyítandó egyenlőtlenség ezek alapján: $\begin{array}{c}{\displaystyle \frac{2T}{b+c-a}\ge \frac{3abc}{8T}\mathrm{.}}\end{array}$ Átszorzás után a $16T^2$ helyére a Heron-képlet alapján beírhatjuk, hogy $\begin{array}{c}{\displaystyle \left(a+b+c\right)\left(a+b-c\right)\left(a-b+c\right)\left(-a+b+c\right)\mathrm{.}}\end{array}$ A háromszög-egyenlőtlenség szerint $b+c>a$, azaz $b+c-a$ pozitív, így egyszerűsíthetünk vele. Így a bizonyítandó állítás: $\begin{array}{c}{\displaystyle \left(a+b+c\right)\left(a+b-c\right)\left(a-b+c\right)\ge 3abc\mathrm{.}}\end{array}$ (Itt is látható, hogy ez az állítás szimmetrikus a $b$ és $c$ változókra, tehát $b\ge c$ valóban feltehető.) Most helyettesítsük az oldalakat a bizonyítandó egyenlőtlenségben a beírt kör által levágott érintőszakaszokkal, vagyis legyen $s-a=x\mathrm{,}s-b=y$ és $s-c=z$. A háromszög-egyenlőtlenség miatt ezek mind pozitívak. Feltettük, hogy $a\ge b\ge c$, ennek megfelelően $z\ge y\ge x$ is igaz. A helyettesítés után: $\begin{array}{c}{\displaystyle 2\left(x+y+z\right)\cdot 2y\cdot 2z\ge 3\left(x+y\right)\left(y+z\right)\left(z+x\right)\mathrm{.}}\end{array}$ A zárójelek fölbontása és a kifejezések összevonása után: $\begin{array}{c}{\displaystyle 2xyz+5y^{2}z+5y{z}^2\ge 3x^{2}y+3x{y}^2+3z^{2}x+3z{x}^2\mathrm{.}}\end{array}$ Felírhatunk több egyenlőtlenséget, amelyek a $z\ge y\ge x$ feltételből azonnal következnek: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 2xyz}& {\displaystyle \ge 2x{y}^2\mathrm{,}}\hfill \\ \hfill {\displaystyle 3y{z}^2}& {\displaystyle \ge 3x{z}^2\mathrm{,}}\hfill \\ \hfill {\displaystyle 3y^{2}z}& {\displaystyle \ge 3x^{2}z\mathrm{,}}\hfill \\ \hfill {\displaystyle y^{2}z}& {\displaystyle \ge x{y}^2\mathrm{,}}\hfill \\ \hfill {\displaystyle y^{2}z}& {\displaystyle \ge x^{2}y\mathrm{,}}\hfill \\ \hfill {\displaystyle 2y{z}^2}& {\displaystyle \ge 2x^{2}y\mathrm{.}}\hfill \end{array}}$ Ezeket összeadva éppen a bizonyítandó állítást kapjuk, és mivel ekvivalens átalakításokat végeztünk, ezért az eredeti is igaz. Egyenlőség csakis úgy teljesülhet, ha $x=y=z$, vagyis a háromszög szabályos.    Tubak Dániel (Szegedi Radnóti Miklós Kís. Gimn., 10. évf.)  dolgozata alapján 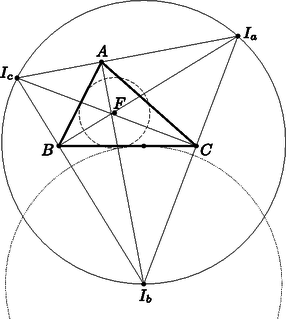    II. megoldás. Jelölje szokásosan $a$, $b$, $c$ az oldalakat, $s$ a félkerületet, $R$ a köréírt kör sugarát, továbbá $r_a$, $r_b$, $r_c$ a kozzáírt körök sugarait, $F$ a Feuerbach-kör középpontját, $O$ a köréírt kör középpontját, $I_a$, $I_b$, $I_c$ pedig a hozzáírt körök középpontjait. $F{I}_a=\frac{R}{2}+r_a$, hiszen a Feuerbach-kör sugara $\frac{R}{2}$, továbbá a Feuerbach-kör érinti a hozzáírt köröket. Ezért hasonlóan $F{I}_b=\frac{R}{2}+r_b\mathrm{,}F{I}_c=\frac{R}{2}+r_c$. Rövid számolással belátható, hogy a hozzáírt körök középpontjaiból álló háromszög szögei $\frac{\alpha +\beta }{2}$, $\frac{\beta +\gamma }{2}$, $\frac{\gamma +\alpha }{2}$ (ahol $\alpha$, $\beta$, $\gamma$ a háromszög szögei), így ez a háromszög hegyesszögű. A hozzááírt körök középpontjaiból rajzolt háromszög magasságainak talppontjai $A$, $B$, $C$, így e háromszög Feuerbach-köre éppen az $ABC$ háromszög köréírt köre, melynek sugara $R$ ‐ vagyis az $I_a{I}_b{I}_c$ háromszög köréírt körének sugara $2R$. Legyen ennek a körnek a középpontja $G$. A $G$ az $I_a{I}_b{I}_c$ háromszögön belül van, hiszen ez a háromszög hegyesszögű. A síkon ez az egyetlen pont, amely az $I_a$, $I_b$, $I_c$ pontok mindegyikétől legfeljebb $2R$ távolságra van, ugyanis ha vennénk az $I_a$, $I_b$ és $I_c$ középpontú $2R$ sugarú köröket, akkor azoknak még további közös pontja is lenne, de mivel a körvonalaik $G$-ben közösen metszik egymást és a köréírt kör középpontja egyértelmű (nincs a körvonalaknak még egy közös metszéspontja), ezért $G$ az egyetlen ilyen pont. Így van olyan körközéppont, mondjuk $I_a$ úgy, hogy $F{I}_a>2R$, azaz $\begin{array}{c}{\displaystyle \frac{R}{2}+r_a\ge 2R\iff r_a\ge \frac{3}{2}R\mathrm{.}}\end{array}$ Egyenlőség pontosan akkor van, ha $F$ és $G$ egybeesik. Az $I_a$, $I_b$ és $I_c$ középpontú hozzáírt körök sugarai általában különbözőek. A $G$ pont az $I_a{I}_b{I}_c$ háromszög körülírt körének középpontja, az eredeti $F$ középpontú Feuerbach-kör pedig mindhárom hozzáírt kört kívülről érinti. Az $F$ és $G$ pontok tehát akkor eshetnek egybe, ha az $F$ pont is egyenlő távolságra van mindegyik hozzáírt kör középpontjától, tehát a három kör sugara egyenlő, vagyis az eredeti háromszög szabályos.    Kerekes Anna (Budapesti Fazekas M. Gyak. Ált. Isk. és Gimn., 11. évf.)  dolgozata alapján