Feladat: B.4947 Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Beke Csongor ,  Dobák Dániel ,  Fitos Bence ,  Füredi Erik Benjámin ,  Gáspár Attila ,  Hegedűs Dániel ,  Kerekes Anna ,  Nagy Nándor ,  Schrettner Jakab ,  Shuborno Das ,  Szabó Dávid ,  Weisz Máté ,  Zsigri Bálint 
Füzet: 2019/március, 148 - 150. oldal  PDF  |  MathML 
Témakör(ök): Feladat, Térgeometriai bizonyítások, Tetraéderek, Kocka
Hivatkozás(ok):Feladatok: 2018/március: B.4947

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen a kocka ABCDA'B'C'D', aminek ABCD és A'B'C'D' két párhuzamos lapja, továbbá az általánosság megszorítása nélkül tegyük fel, hogy térfogata egységnyi. Tegyük fel továbbá, hogy a kockát a Δ1, Δ2, Δ3, Δ4 és Δ5 tetraéderekre daraboltuk. Az ABCD és A'B'C'D' négyzetlapokat a tetraéderek háromszöglapjai lefedik, emiatt mindkettőre legalább két-két lap illeszkedik, továbbá mivel ABCD és A'B'C'D' párhuzamosak, így bármely tetraédernek legfeljebb az egyikre illeszkedhet lapja. Következésképpen két eset lehetséges: az ABCD és A'B'C'D' egyikét pontosan kettő, másikát pontosan három háromszöglap fedi, vagy mindkettőt pontosan kettő háromszöglap fedi.
Tegyük fel, hogy Δ1 és Δ2 egy-egy lapja együttesen lefedi ABCD-t. Nevezzük ezeket az ABCD-re illeszkedő lapokat rendre L1-nek és L2-nek, az ezekhez tartozó magasságokat pedig rendre m1-nek és m2-nek. Világos, hogy L1 és L2 területeinek összegére T(L1)+T(L2)=1, valamint m1≤1 és m2≤1 teljesül. Ebből megbecsülhetjük térfogataik összegét:

V(Δ1)+V(Δ2)=T(L1)m1+T(L2)m23≤T(L1)+T(L2)3=13.
Teljesen hasonlóan megmutatható, hogy ha három tetraéder lapjai fedik ABCD-t, akkor a három tetraéder térfogatának összege szintén legfeljebb 13, és ugyanezen megállapítások érvényesek az A'B'C'D' lapra is.
Ezen térfogatbecslések alapján nem fordulhat elő az az eset, amikor az ABCD és A'B'C'D' egyikét pontosan kettő, másikát pontosan három háromszöglap fedi, hiszen ekkor az öt tetraéder térfogatának összege legfeljebb 13+13=23<1 lenne. Vagyis (esetleges átindexelés után) feltehetjük, hogy Δ1 és Δ2 lapjai együttesen lefedik ABCD-t, és Δ3 és Δ4 lapjai együttesen lefedik A'B'C'D'-t. Ismét a térfogatbecslések miatt
V(Δ1)+V(Δ2)≤13ésV(Δ3)+V(Δ4)≤13,
így viszont V(Δ5)≥13.
Világos, hogy ABCD és A'B'C'D' helyett bármely párhuzamos lappárra működik az érvelésünk, azaz bármely négyzetlapját a kockának pontosan két tetraéder egy-egy háromszöglapja fedi. Továbbá ha feltesszük, hogy valamely lap fedésében Δ5 is részt vesz, mondjuk Δi párjaként, akkor a térfogatbecslés miatt V(Δ5)+V(Δi)≤13, ami ellentmond V(Δ5)≥13 következtetésünknek. Kaptuk tehát, hogy Δ5-nek nincs közös lapsíkja a kockával, a Δ1, Δ2, Δ3, Δ4 tetraéderek mindegyikének pedig pontosan három (mind a három párhuzamos lappárból egy-egy).
Vizsgáljuk most Δ1-et. Egy négyzetet pontosan két háromszögre csak egy átlójával vághatunk, ebből következően Δ1-nek a kocka lapjaira illeszkedő három lapja egy-egy egységnyi befogójú egyenlőszárú derékszögű háromszög. Mivel ezeknek a lapoknak páronként van egy-egy közös élük, így Δ1 szükségképpen egy ,,saroktetraéder'', azaz egy olyan tetraéder, amelynek négy csúcsa a kocka egy csúcsából kiinduló három élének négy végpontja. Ugyanezen érvelés helyes Δ2, Δ3 és Δ4 esetén is.
Végül világos, hogy Δ5-nek Δ1, Δ2, Δ3, Δ4 mindegyikével egy-egy 2 oldalhosszúságú szabályos háromszög a közös lapja, vagyis Δ5 egy 2 élhosszúságú szabályos tetraéder.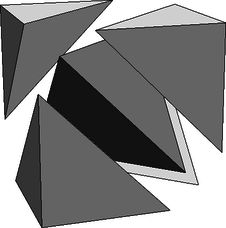

Jól ismert és az ábra alapján könnyen látható, hogy egy kocka valóban felbontható 5 tetraéderre. Ezzel az állítást beláttuk.