Kezdőlap


Feladat:	B.4915	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	2019/február, 87 - 88. oldal		PDF \| MathML
Témakör(ök):	Feladat, Ponthalmazok, Kombinatorikus geometria
Hivatkozás(ok):	Feladatok: 2017/december: B.4915

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelölje $h^{A_{i}}$ ( $i = 1,2,3,4,5$ ) azon háromszögek számát, amelyeknek minden csúcsa az ${A_{1}, A_{2}, A_{3}, A_{4}, A_{5}} ∖ {A_{i}}$ pontok valamelyike, és tartalmazzák $P$ -t. Így minden $P$ -t tartalmazó háromszöget pontosan kettő $h^{A_{i}}$ -ben számolunk meg, pl. ha $P \in A_{1} A_{2} A_{3} ▵$ , akkor az $A_{1} A_{2} A_{3} ▵$ -et megszámoltunk $h^{A_{4}}$ és $h^{A_{5}}$ kiszámítása közben. Következésképpen 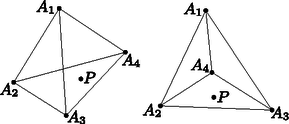$k_{3} = (h^{A_{1}} + ... + h^{A_{5}}) / 2$ .
Most tegyük fel, hogy $P$ benne van az $A_{1}$ , $A_{2}$ , $A_{3}$ , $A_{4}$ pontok konvex burkában. A négy általános helyzetű pont konvex burka lehet négyszög vagy háromszög. Mindkét esetben könnyen láthatjuk, hogy a $P$ pont pontosan két olyan háromszögben van benne, amelynek csúcsai $A_{1}$ , $A_{2}$ , $A_{3}$ , $A_{4}$ közül valók.

Az ábrán látható első esetben pontosan az

A_{1} A_{3} A_{4} ▵

és az

A_{2} A_{3} A_{4} ▵

tartalmazza

P

-t, a második esetben pedig pontosan az

A_{1} A_{2} A_{3} ▵

és az

A_{2} A_{3} A_{4} ▵

. Világos, hogy

P

-t a lérejövő tartományok másikába helyezve is mindig pontosan két háromszög fogja tartalmazni. Kaptuk, hogy

h^{A_{5}} = 2

, ha

P

benne van az

A_{1}

A_{2}

A_{3}

A_{4}

pontok konvex burkában; és nyilvánvalóan

h^{A_{5}} = 0

, ha

P

nincs benne az

A_{1}

A_{2}

A_{3}

A_{4}

pontok konvex burkában.
Az érvelésben

A_{5}

szerepe lényegtelen, azaz általában is igaz, hogy

h^{A_{j}}

értéke

2

, ha

P

A_{j}

elhagyása után megmaradt négy pont konvex burkába esik, egyébként pedig

0

. Eszerint a

h^{A_{1}} + ... + h^{A_{5}}

összeg pontosan a kétszerese azon pontnégyesek számának, amelyek konvex burka tartalmazza

P

-t, azaz

h^{A_{1}} + ... + h^{A_{5}} = 2 k_{4}

.
Így

k_{3} = (h^{A_{1}} + ... + h^{A_{5}}) / 2 = k_{4}

, amivel az állítást beláttuk.