Feladat:	2018. évi Kürschák matematikaverseny 1. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Füzet:	2019/február, 67 - 69. oldal		PDF  |  MathML
Témakör(ök):	Kürschák József (korábban Eötvös Loránd), Síkgeometriai bizonyítások, Beírt kör, Súlyvonal
Hivatkozás(ok):	Feladatok: 2019/február: 2018. évi Kürschák matematikaverseny 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Ha $|AB|=|AC|$, akkor az ábra szimmetrikus az $A$-ból induló magasságra, amely egyben súlyvonal is. Ezért az $A_1$ és az $M$ pont is ezen a szimmetriatengelyen fekszik, így az állítás triviális. A továbbiakban feltesszük, hogy $|AB|\ne |AC|$. Ekkor az $A$-ból induló szögfelező nem merőleges a $BC$ oldalra, tehát az $AB$-nek egy, a $BC$-re merőleges egyenesre vett tükörképe nem párhuzamos $AC$-vel. Legyen $K$ az $ABC$ háromszög beírt körének középpontja, és jelölje $A\text{'}$, $B\text{'}$ és $C_1\text{'}$ rendre az $A$, $B$, illetve $C_1$ pontoknak az $A_{1}K$ egyenesre vett tükörképét. Láttuk, hogy $AC$ és $A\text{'}B\text{'}$ nem párhuzamosak, ezért egyértelműen létezik az $AC$ és $A\text{'}B\text{'}$ egyeneseknek egy $P\text{'}$ metszéspontja. Legyen $P$ a $P\text{'}$-nek az $A_{1}K$-ra vett tükörképe, valamint jelölje $N$ a $PP\text{'}$ és $A_{1}K$ metszéspontját (1. ábra). 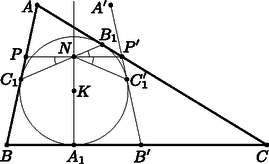    1. ábra   Ekkor $KNP\text{'}\sphericalangle ={90}^{\circ }$ a tükrözés miatt, illetve $K{B}_{1}P\text{'}\sphericalangle =K{C}_1\text{'}P\text{'}\sphericalangle ={90}^{\circ }$, hiszen $P\text{'}{B}_1$ és $P\text{'}{C}_1\text{'}$ a beírt kör érintői. Ezek szerint $K$, $N$, $B_1$, $P\text{'}$ és $C_1\text{'}$ egy $k$ körön vannak, konkrétan a $KP\text{'}$ Thálesz-körén. Ezen $k$ körnek $P\text{'}{B}_1$ és $P\text{'}{C}_1\text{'}$ egyenlő hosszúságú húrjai (mivel mindkét szakasz a beírt körnek ugyanabból a $P\text{'}$ külső pontból húzott érintője), tehát $k$-ban ugyanakkora kerületi szögek tartoznak hozzájuk: $B_{1}NP\text{'}\sphericalangle =C_1\text{'}NP\text{'}\sphericalangle =C_{1}NP\sphericalangle$; az utóbbi egyenlőség a tükrözés miatt igaz. Ezek szerint $N$ illeszkedik a $C_1{B}_1$ szakaszra. $BC\perp A_{1}K\perp PP\text{'}$ miatt $BC\parallel PP\text{'}$ és $|PN|=|P\text{'}N|$ a tükrözésből adódóan. Alkalmas, $A$-ból végzett középpontos hasonlóság tehát $PP\text{'}$-t $BC$-be és $N$-et a $BC$ szakasz felezőpontjába viszi. Ez pedig azt jelenti, hogy $N$ rajta van az $ABC$ háromszög $A$-ból induló súlyvonalán. Az $N$ pont tehát megegyezik a $B_1{C}_1$ szakasznak és az $ABC$ háromszög $A$-ból induló súlyvonalának metszéspontjával, $M$-mel, ahonnan $A_{1}M=A_{1}N\perp BC$ adódik. Nekünk pedig pontosan ezt kellett igazolunk. 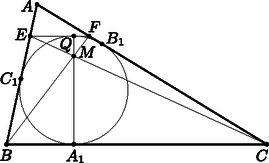 $\square$   Az alábbiakban közöljük Egri Máté rendkívül szellemes megoldásának vázlatát is.   II. megoldás. Jelölje $Q$ az $ABC$ háromszög beírt körének $A_1$-gyel átellenes pontját, és legyenek rendre $E$ és $F$ a beírt körhöz $Q$-ban húzott (és $BC$-vel párhuzamos) érintőnek az $AB$ és $AC$ oldalakkal vett metszéspontjai (2. ábra).     2. ábra   Azt fogjuk megmutatni, hogy az $M$ pont egyrészt megegyezik $EC$ és $BF$ metszéspontjával, másrészt, hogy illeszkedik az $A_{1}Q$ szakaszra. A konstrukció folytán $EBCF$ trapéz, így átlóinak metszéspontját a szárak metszéspontjával (azaz $A$-val) összekötő egyenes felezi az alapokat. Ez azt jelenti, hogy $EC$ és $BF$ metszéspontja illeszkedik az $A$-ból induló súlyvonalra. A továbbiakban a jól ismert Brianchon-tételre támaszkodunk, amely szerint egy érintőhatszög szemközti csúcsait összekötő három átló egy ponton halad át. A tételt abban az elfajuló esetben alkalmazzuk, amikor az érintőhatszög bizonyos csúcsai a hatszög beírt körén vannak. Ilyenformán az $E{C}_{1}BC{B}_{1}F$ elfajuló érintőhatszög fenti tulajdonsága alapján $C_1{B}_1$ tartalmazza $EC$ és $BF$ metszéspontját, amely ‐ mint láttuk ‐ az $A$-ból induló súlyvonalon van. Tehát $EC$ és $BF$ valóban az $M$ pontban metszik egymást. Az $EB{A}_{1}CFQ$ érintőhatszögre pedig az adódik, hogy $A_{1}Q$ is tartalmazza $M$-et. A feladat állítása innen közvetlenül adódik. $\square$