Kezdőlap


Feladat:	B.4949	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Janzer Orsolya Lili
Füzet:	2019/január, 25 - 26. oldal		PDF \| MathML
Témakör(ök):	Feladat, Síkgeometriai bizonyítások, Háromszög nevezetes vonalai, Húrnégyszögek, Trapézok
Hivatkozás(ok):	Feladatok: 2018/április: B.4949

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Mivel $B E C ∢$ és $B D C ∢$ derékszög, azért $B C D E$ húrnégyszög. Emiatt a $C B E ∢$ és az $A D E ∢$ szög megegyezik. A $P$ pont az $A D$ szakasz pontja, így a $P D E ∢$ szög is ugyanekkora. Most felhasználjuk, hogy $D P Q E$ is húrnégyszög, ezért $P D E ∢ = P Q A ∢$ . Ezzel két lépésben beláttuk, hogy a $P Q A ∢$ és $C B A ∢$ szögek egyenlők. A feladat feltételei alapján a $P$ és $Q$ pontok az eredeti háromszög oldalain vannak, így az előzőek egyállású szögek, így $P Q$ párhuzamos 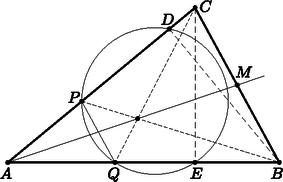$B C$ -vel.

B A C

szögre és a

B C

P Q

párhuzamos egyenesekre alkalmazva a párhuzamos szelők tételét

\begin{matrix} \frac{A Q}{A P} = \frac{B Q}{C P} \Rightarrow A Q \cdot C P = B Q \cdot A P . \end{matrix}

(1)

M

pont a

B C

oldal felezőpontja, tehát

M B = M C

.
Bővítsük (1)-ben a szorzatokat az egymással megegyező

M B

-vel és

M C

-vel:

\begin{matrix} A Q \cdot C P \cdot M B = B Q \cdot A P \cdot C M . \end{matrix}

A B C

háromszögben az

A M

B P

és

C Q

szakaszokra alkalmazható a fenti egyenlőség alapján a Ceva-tétel megfordítása, azaz

A M

B P

és

C Q

egy pontban metszik egymást. Az

A M

a háromszög

A

-hoz tartozó súlyvonala, így az állítást igazoltuk.

Janzer Orsolya Lili (Budapesti Fazekas M. Gyak. Ált. Isk. és Gimn., 12. évf.)
dolgozata alapján