Kezdőlap


Feladat:	B.4941	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Csépányi István
Füzet:	2018/december, 539 - 540. oldal		PDF \| MathML
Témakör(ök):	Feladat, Síkgeometriai bizonyítások, Körülírt kör, Húrnégyszögek, Középpontos és egyéb hasonlósági transzformációk
Hivatkozás(ok):	Feladatok: 2018/március: B.4941

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az ábra jelölései szerint legyenek a magasságok talppontjai $T_{A}$ , $T_{B}$ , $T_{C}$ . Az $O$ középpont $T_{A}$ , $T_{B}$ és $T_{C}$ pontokra vonatkozó tükörképei rendre $D$ , $E$ és $F$ , továbbá a magasságpont oldalakra (és így a magasságok talppontjaira) vonatkozó tükörképei pedig 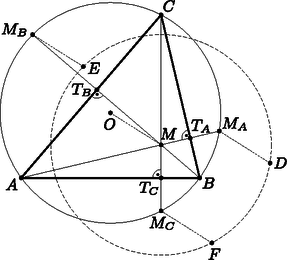$M_{A}$ , $M_{B}$ és $M_{C}$ .
Ismert, hogy a háromszög magasságpontját az oldalakra tükrözve a kapott $M_{A}$ , $M_{B}$ , $M_{C}$ pontok rajta vannak az $A B C$ háromszög körülírt körén.

Tekintsük ezután a

D

és

M_{A}

pontokat. A

D

pont az

O

pontnak, az

M_{A}

pont pedig

M

pontnak a

T_{A}

talppontra vonatkozó tükörképei, így az

M O M_{A} D

négyszög középpontosan szimmetrikus, tehát paralelogramma. Így

\vec{O M} = \vec{M_{A} D}

. Most az

O

és

M

pontokat a

T_{B}

talppontra tükrözve látjuk azt is, hogy

\vec{O M} = \vec{M_{B} E}

. Végül a

T_{C}

-re tükrözve

O

-t és

M

-et ismét a paralelogrammma tulajdonságából

\vec{O M} = \vec{M_{C} F}

.
E három vektor azt jelenti, hogy a

D E F

háromszög az

M_{A} M_{B} M_{C}

háromszög eltoltja az

\vec{O M}

vektorral. A két háromszög egybevágó, a körülírt köreik sugara megegyezik, ráadásul a

D E F

háromszög körülírt körének középpontja az eredeti

A B C

háromszög magasságpontja.

Csépányi István (Egri Szilágyi Erzsébet Gimnázium, 11. évf.)
dolgozata alapján