Feladat:	2018. évi Nemzetközi Matematika Diákolimpia 23. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Gáspár Attila
Füzet:	2018/november, 453 - 454. oldal		PDF  |  MathML
Témakör(ök):	Nemzetközi Matematikai Diákolimpia, Síkgeometriai bizonyítások, Síkgeometriai számítások trigonometriával
Hivatkozás(ok):	Feladatok: 2018/szeptember: 2018. évi Nemzetközi Matematika Diákolimpia 23. feladata

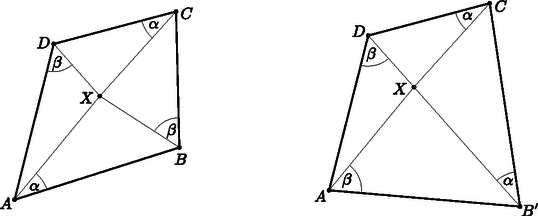
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Gáspár Attila megoldása. Legyen $XAB\sphericalangle =XCD\sphericalangle =\alpha$ és $XBC\sphericalangle =XDA\sphericalangle =\beta$. Vegyük fel a $B\text{'}$ pontot az ábra szerint úgy, hogy $XB\text{'}=\frac{XA\cdot XC}{XB}$ és $AXB\text{'}\sphericalangle =BXC\sphericalangle$. Ekkor $\begin{array}{c}{\displaystyle \frac{AX}{B\text{'}X}=\frac{AX\cdot XB}{XA\cdot XC}=\frac{XB}{XC}m}\end{array}$ ezért $AXB\text{'}\sim BXC$. Emiatt $B\text{'}AX\sphericalangle =CBX\sphericalangle =\beta$, és $AB\text{'}=BC\cdot \frac{AX}{BX}$.     ${\displaystyle \begin{array}{cc}\hfill {\displaystyle B\text{'}XC\sphericalangle }& {\displaystyle =AXB\text{'}\sphericalangle +B\text{'}XC\sphericalangle -AXB\text{'}\sphericalangle =}\hfill \\ \hfill {\displaystyle }& {\displaystyle =AXB\sphericalangle +BXC\sphericalangle -BXC\sphericalangle =AXB\sphericalangle \mathrm{,}\text{és}}\hfill \\ \hfill {\displaystyle \frac{B\text{'}X}{CX}}& {\displaystyle =\frac{XA\cdot XC}{XB\cdot XC}=\frac{XA}{XB}\mathrm{,}}\hfill \end{array}}$ ezért $B\text{'}XC\sim AXB$. Így $XB\text{'}C\sphericalangle =\alpha$ és $B\text{'}C=AB\cdot \frac{XC}{XB}$. Látható, hogy $DCB\text{'}\sphericalangle =\alpha +XCB\text{'}\sphericalangle ={180}^{\circ }-B\text{'}XC\sphericalangle$, ezért $\text{sin}DCB\text{'}\sphericalangle =\text{sin}BXC\text{'}\sphericalangle$. Ebből következik, hogy ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle \frac{T_{B\text{'}CD}}{T_{XB\text{'}C}}}& {\displaystyle =\frac{DC\cdot CB\text{'}\cdot \text{sin}DCB\text{'}\sphericalangle }{B\text{'}X\cdot XC\cdot \text{sin}B\text{'}XC\sphericalangle }=\frac{DC\cdot CB\text{'}}{B\text{'}X\cdot XC}=}\hfill & \text{(<mn>1</mn>)}\\ \hfill {\displaystyle }& {\displaystyle =\frac{DC\cdot AB\cdot \frac{XC}{XB}}{B\text{'}X\cdot XC}=\frac{CD\cdot AB}{XB\text{'}\cdot XB}\mathrm{.}}\hfill \end{array}}$ A területeket másképp felírva $\begin{array}{c}{\displaystyle \frac{T_{B\text{'}CD▵}}{T_{XB\text{'}C▵}}=\frac{B\text{'}D\cdot B\text{'}C\cdot \text{sin}CB\text{'}D\sphericalangle }{B\text{'}X\cdot B\text{'}C\cdot \text{sin}\alpha }=\frac{B\text{'}D}{B\text{'}X}\cdot \frac{\text{sin}CB\text{'}D\sphericalangle }{\text{sin}\alpha }\mathrm{.}}\end{array}$ (2) Az $\left(1\right)$ és $\left(2\right)$ egyenletet összevetve kapjuk, hogy ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \frac{CD\cdot AB}{XB\text{'}\cdot XB}}& {\displaystyle =\frac{B\text{'}D}{B\text{'}X}\cdot \frac{\text{sin}CB\text{'}D\sphericalangle }{\text{sin}\alpha }\mathrm{,}}\hfill \\ \hfill {\displaystyle \frac{CD\cdot AB}{B\text{'}D\cdot XB}}& {\displaystyle =\frac{\text{sin}CB\text{'}D\sphericalangle }{\text{sin}\alpha }\mathrm{.}}\hfill & \text{(<mn>3</mn>)}\end{array}}$ Hasonlóan látható, hogy ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle \frac{T_{DAB\text{'}▵}}{T_{XDA▵}}}& {\displaystyle =\frac{AD\cdot AB\text{'}}{DX\cdot XA}=\frac{AD\cdot BC}{DX\cdot BX}\mathrm{,}}\hfill & \text{(<mn>4</mn>)}\\ \hfill {\displaystyle \frac{T_{DAB\text{'}▵}}{T_{XDA▵}}}& {\displaystyle =\frac{B\text{'}D}{DX}\cdot \frac{\text{sin}ADB\text{'}\sphericalangle }{\text{sin}\beta }\mathrm{.}}\hfill & \text{(<mn>5</mn>)}\end{array}}$ A $\left(4\right)$ és $\left(5\right)$ egyenletből kapjuk, hogy ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \frac{AD\cdot BC}{DX\cdot BX}}& {\displaystyle =\frac{B\text{'}D}{DX}\cdot \frac{\text{sin}ADB\text{'}\sphericalangle }{\text{sin}\beta }\mathrm{,}}\hfill \\ \hfill {\displaystyle \frac{AD\cdot BC}{B\text{'}D\cdot XB}}& {\displaystyle =\frac{\text{sin}ADB\text{'}\sphericalangle }{\text{sin}\beta }\mathrm{.}}\hfill & \text{(<mn>6</mn>)}\end{array}}$ $AB\cdot CD=AD\cdot BC$, ezért a $\left(3\right)$ és $\left(6\right)$ egyenlet miatt $\begin{array}{c}{\displaystyle \frac{\text{sin}CB\text{'}D\sphericalangle }{\text{sin}\alpha }=\frac{\text{sin}ADB\text{'}\sphericalangle }{\text{sin}\beta }\mathrm{.}}\end{array}$ (7) Tegyük fel, hogy $X\notin B\text{'}D$. A szimmetria miatt feltételezhetjük, hogy $X$ a $B\text{'}CD$ háromszögben van. Ekkor $CB\text{'}D\sphericalangle >\alpha$, ezért $\text{sin}CB\text{'}D\sphericalangle >\text{sin}\alpha$, és $ADB\text{'}\sphericalangle <\beta$, ezért $\text{sin}ADB\text{'}\sphericalangle <\text{sin}\beta$. Ez ellentmond a $\left(7\right)$ egyenletnek. Tehát $X$ a $B\text{'}D$ szakaszon van. Ebből a feladat állítása könnyen adódik, mert $\begin{array}{c}{\displaystyle BXA\sphericalangle +DXC\sphericalangle =B\text{'}XC\sphericalangle +CXD\sphericalangle ={180}^{\circ }\mathrm{.}}\end{array}$   Megjegyzés. Ha $0^{\circ }<{\phi }_1<{\phi }_2<{180}^{\circ }$, akkor csak abban az esetben lehetséges, hogy $\text{sin}{\phi }_1\ge \text{sin}{\phi }_2$, ha ${\phi }_1+{\phi }_2\ge {180}^{\circ }$. Látható, hogy $CB\text{'}D\sphericalangle +\alpha <CB\text{'}D\sphericalangle +\alpha +XCB\text{'}\sphericalangle ={180}^{\circ }-B\text{'}DC\sphericalangle <{180}^{\circ }$, és hasonlóan $ADB\text{'}\sphericalangle +\beta <{180}^{\circ }$. Emiatt ez az eset nem fordulhat elő a fenti bizonyításban.