Kezdőlap


Feladat:	B.4934	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Döbröntei Dávid Bence
Füzet:	2018/október, 411 - 413. oldal		PDF \| MathML
Témakör(ök):	Feladat, Különleges függvények, Legnagyobb közös osztó, Prímtényezős felbontás
Hivatkozás(ok):	Feladatok: 2018/február: B.4934

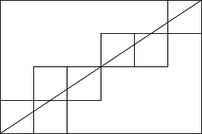
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A bal alsó és a jobb felső csúcsot összekötő átló $n - 1$ vízszintes és $k - 1$ függőleges rácsegyenest metsz a téglalap belsejében. Pontosan akkor halad át egy, a jobb felső sarokban lévőtől különböző (rács) egységnégyzet belsején, ha annak jobb oldali függőleges vagy felső vízszintes oldalát metszi.

E metszéspontok száma összesen

(n - 1) + (k - 1) = n + k - 2

. Azonban két ilyen metszéspont egybe is eshet; ez éppen akkor következik be, amikor az átló a téglalap belsejében lévő rácsponton halad át. Egy ilyen rácspont a téglalap bal alsó csúcsával egy

n_{1} \times k_{1}

-es rácstéglalapot határoz meg, ahol

\frac{n}{n_{1}} = \frac{k}{k_{1}}

, azaz

\begin{matrix} n k_{1} = n_{1} k, és 1 \leq n_{1} < n, 1 \leq k_{1} < k egészek. \end{matrix}

Jelölje

n

és

k

legnagyobb közös osztóját

d

, ekkor

\begin{matrix} n = d n^{*}, k = d k^{*}, aholn^{*}ésk^{*}relatív prímek. \end{matrix}

A korábbi összefüggésbe helyettesítve:

\begin{matrix} d n^{*} k_{1} = n_{1} d k^{*}, azaz n^{*} k_{1} = n_{1} k^{*} . \end{matrix}

Ebből következik, hogy

n_{1} k^{*}

osztható

n^{*}

-gal, ami a relatív prímség miatt csak akkor következik be, ha

n_{1}

osztható

n^{*}

-gal:

n_{1} = x n^{*}

, ahol

x

pozitív egész, és

n^{*} x < n = d n^{*}

miatt

1 \leq x < d

; emiatt

k_{1} = x k^{*}

.
A téglalap átlójára eső belső rácspontok száma tehát megegyezik

x

lehetséges értékeinek számával,

d - 1

-gyel. Ennyi egységnégyzetet az

n + k - 2

formulában kétszer számoltunk, így ‐ az eddig kihagyott jobb felső sarok egységnégyzetével együtt ‐ az átló

(n + k - 2) - (d - 1) + 1 = n + k - d

egységnégyzet belsején halad keresztül.
Feladatunk ilymódon

n + k - d = 2018

pozitív egész megoldásainak számát kérdezi, ahol

(n, k) = d

és

n \geq k

. Mivel

d

n

-nek és a

k

-nak is osztója, azért

d ∣ 2018 = 2 \cdot 1009

. Az 1009 prím, így

d

szóbajövő értékei: 1, 2, 1009 és 2018.

1. Ha

d = 1

, akkor az

n + k = 2019 = 3 \cdot 673

egyenlet

(n, k) = 1

n \geq k \geq 1

megoldásainak számát keressük. A relatív prímség feltétele nélkül a megoldások száma 1009 lenne. Ezek közül azonban nem megfelelőek azok, amelyeknél

n

és

k

is osztható 3-mal, 673-mal vagy 2019-cel. Az ilyen megoldások száma rendre

[\frac{1009}{3}] = 336

[\frac{1009}{673}] = 1

, illetve

[\frac{1009}{2019}] = 0

, így a valamennyi feltételnek eleget tevő megoldások száma ebben az esetben

1009 - (336 + 1) + 0 = 672

2. Ha

d = 2

, akkor az

n + k = 2020 = 2^{2} \cdot 5 \cdot 101

egyenlet

(n, k) = 2

n \geq k \geq 1

megoldásainak számát keressük. Ez nyilván ugyanannyi, mint az

x + y = 1010 = 2 \cdot 5 \cdot 101

egyenlet

(x, y) = 1

x \geq y \geq 1

megoldásainak a száma. Az első esetben alkalmazott számoláshoz hasonlóan ez

\begin{matrix} 505 - ([\frac{505}{2}] + [\frac{505}{5}] + [\frac{505}{101}]) + ([\frac{505}{10}] + [\frac{505}{202}] + [\frac{505}{505}]) - ([\frac{505}{1010}]) = \\ = 505 - 358 + 53 - 0 = 200. \end{matrix}

3. Ha

d = 1009

, akkor az

n + k = 3027 = 3 \cdot 1009

egyenlet

(n, k) = 1009

n \geq k \geq 1

megoldásainak számát keressük. Az előző esethez hasonlóan ez ugyanannyi, mint az

x + y = 3

egyenlet

(x, y) = 1

x \geq y \geq 1

megoldásainak a száma, ami nyilván 1.

4. Ha

d = 2018

, akkor az

n + k = 4036 = 4 \cdot 1009

egyenlet

(n, k) = 2018

n \geq \geq k \geq 1

megoldásainak számát keressük, ami 1, hiszen csak

n = k = 2018

felel meg.

A négy esetet összegezve, a feladatnak eleget tevő számpárok száma

672 + 200 + 1 + 1 = 874

Döbröntei Dávid Bence (Pápa, Türr István Gimn. és Koll., 12. évf.)
megoldását felhasználva

Megjegyzés. Ha az

m \geq 2

egész prímtényezős alakja

n = p_{1}^{a_{1}} \cdot p_{2}^{a_{2}} \cdot ... \cdot p_{k}^{a_{k}}

, akkor bármely

m

darab egymást követő egész szám közül az

m

-hez relatív prímek száma

φ (m) = p_{1}^{a_{1} - 1} (p_{1} - 1) \cdot p_{2}^{a_{2} - 1} (p_{2} - 1) \cdot ... \cdot p_{k}^{a_{k} - 1} (p_{k} - 1)

. (Ezt a megoldásban is többször használt szita formula segítségével (is) bizonyíthatjuk.) A fenti megoldásban mind a négy esetben egy

x + y = m

típusú egyenlet olyan egész megoldásainak számát kerestük, ahol

(x, y) = 1

és

x \geq y \geq 1

. Itt

1 \leq y \leq [\frac{m}{2}]

, és az

(x, y) = 1

feltétel pontosan akkor teljesül, ha

(y, m) = 1

. Ennek figyelembevételével több megoldó is a

φ (m)

képletének alkalmazásával ért célba.