Kezdőlap


Feladat:	B.4920	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Szabó Dávid
Füzet:	2018/október, 410 - 411. oldal		PDF \| MathML
Témakör(ök):	Feladat, Kombinatorikus geometria, Sík parkettázás
Hivatkozás(ok):	Feladatok: 2017/december: B.4920

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Először teljes indukcióval azt igazoljuk, hogy egy $2 \times n$ -es téglalapot $1 \times 2$ -es dominókkal $F_{n + 1}$ -féleképpen lehet lefedni, ahol $F_{n + 1}$ a Fibonacci-sorozat $(n + 1)$ -edik tagját jelöli 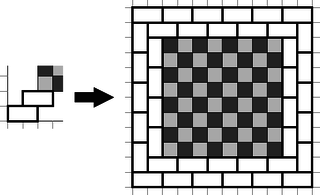$(F_{1} = 1, F_{2} = 1)$ .
A $2 \times 1$ -es téglalap egyféleképpen fedhető le ( $F_{2} = 1$ ), a $2 \times 2$ -es pedig kétféleképpen (2 vízszintes, vagy 2 függőleges, $F_{3} = 2$ ). Tegyük fel, hogy az állítás igaz minden $2 \times k$ méretű téglalapra, ahol $k < n$ . Tekintsük egy $2 \times n$ -es téglalap lehetséges lefedéseit és bontsuk ezeket két csoportra attól függően, hogy a bal alsó sarkuk milyen állású dominóval van lefedve. (Mivel sarokban van, csak kétféleképpen lehet.) Ha függőleges ez a dominó, akkor a megmaradó rész $2 \times (n - 1)$ -es, amit az indukciós feltevés miatt $F_{n}$ -féleképpen lehet lefedni. Ha vízszintes, akkor a bal felső sarkot már csak egyféleképpen tudjuk lefedni, egy vízszintes dominóval. Ha ezt a 2 dominót letesszük, a megmaradó rész $2 \times (n - 2)$ -es, amit $F_{n - 1}$ -féleképpen lehet lefedni. Ezzel minden esetet megvizsgáltunk, tehát egy $2 \times n$ -eset $F_{n} + F_{n - 1} = F_{n + 1}$ -féleképen lehet lefedni.
Most térjünk át a feladatra. Ha lefedjük egy sarkát, és melléteszünk egy vele párhuzamosat 1-gyel elcsúsztatva (lásd 1. ábra), akkor a lefedést már csak egyféleképpen fejezhetjük be, mert mindig lesz egy nem lefedett mező, amit az addig lerakottak miatt csak egyféleképpen lehet lefedni (pl: a legalsó sor 3. négyzete).

1. ábra

Ilyen lefedésből összesen 2 van, mivel a sarkot, ahol kezdtük az eljárást függőleges és vízszintes dominóval is le lehet fedni. (Ha a másikat választjuk, akkor a fenti ábra

90^{\circ}

-os elforgatottját kapjuk, és akármelyik csúcsnál kezdjük, ennek a két lefedésnek a valamelyikét kapjuk.) Vagyis ha ezeket nem nézzük, akkor a lefedésekben nem fordulhat elő olyan, ami az 1. ábra bal oldalán van, azaz a többi esetben miután minden sarkot lefedtünk, a maradék részt felbonthatjuk

2 \times n

-es téglalapokra (2. ábra, az ábrán behúzott szakaszokat nem takarhatja dominó).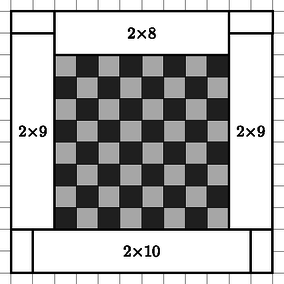

2. ábra

Így a sakktábla minden oldalához eredetileg egy

2 \times 8

-as téglalap tartozik, és a sakktábla mind a négy sarkára lehelyezett

1 \times 2

-es dominó ezek közül valamelyiknek az oldalát 1-gyel megnöveli. Így tartozhat

2 \times 8

-as,

2 \times 9

-es és

2 \times 10

-es téglalap egy-egy oldalhoz, de sem két

2 \times 8

-as, sem két

2 \times 10

-es nem tartozhat szomszédos oldalakhoz. Ezeket a feltételeket figyelembe véve nézzük meg, hogy mekkorák lehetnek az oldalakhoz tartozó téglalapok.
Ha van két 10-es, akkor azok csak egymással szemben lehetnek, a másik kettő pedig 8-as, mert a két 10-es ,,elhasználta'' a sarkok növelését. A 10-es oldalpár kétféleképpen helyezkedhet el.
Ha egy 10-es van, akkor a többi három csak két 9-esből és egy 8-asból állhat (különben nem jönne ki a sarkok által nyújtott 4 növelés). A 10-es oldalt 4-féleképpen, majd a 8-ast 3-féleképpen helyezhetjük le, ez

3 \cdot 4 = 12

lehetőség.
Ha nincs 10-es, akkor mindegyik 9-es (különben nem lenne meg a sarkok által nyújtott 4 növelés). Ekkor a sarkok

90^{\circ}

-os forgásszimmetriával rendelkeznek, így ha az egyiket megválasztjuk, az meghatározza a többit. Ebből az esetből tehát 2 van.
Minden sávot külön-külön kell lefedni, vagyis össze kell szorozni az egyes lefedhetőségeket. Tehát az eredeti alakzatot összesen

\begin{matrix} 2 + 2 \cdot F_{11} \cdot F_{11} \cdot F_{9} \cdot F_{9} + 12 \cdot F_{11} \cdot F_{10} \cdot F_{10} \cdot F_{9} + 2 \cdot F_{10} \cdot F_{10} \cdot F_{10} \cdot F_{10} = \\ = 2 + 2 \cdot 89^{2} \cdot 34^{2} + 12 \cdot 89 \cdot 55^{2} \cdot 34 + 2 \cdot 55^{4} = 146 458 404 \end{matrix}

különböző módon fedhetjük le.

Szabó Dávid (Budapesti Fazekas M. Gyak. Ált. Isk. és Gimn., 11. évf.)
dolgozata alapján