Kezdőlap


Feladat:	642. fizika gyakorlat	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	(G. P.) , Bányai Kristóf , Markó Péter , Tallósy Péter
Füzet:	2019/január, 50 - 52. oldal		PDF \| MathML
Témakör(ök):	Gyakorlat, Csúszásmentes (tiszta) gördülés
Hivatkozás(ok):	Feladatok: 2018/szeptember: 642. fizika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük a nagy kör középpontját

O

-val, az a pontja pedig, amelyiket a kerék kijelölt kerületi pontja

(M)

valamikor (a kezdőhelyzetnek tekintett pillanatban) elért, legyen

A

. Megmutatjuk, hogy az

M

pont az

O A

sugárhoz tartozó átmérőn mozog oda-vissza.
Ha a kis kerék középpontja a kezdőhelyzethez képest

φ

szöggel elfordul a nagy kör középpontja körül, a két kör érintési pontja

B

-be kerül (1. ábra). A kis kör és az

O M

egyenes metszéspontja az egyenlő szárú

O O_{1} M

háromszöget jelöli ki, amelynek

O_{1}

-nél levő külső szöge

2 φ

. Így a

B M

körív hossza megegyezik a

B A

körív hosszával, hiszen a sugarak aránya

1 : 2

. Az

M

pont tehát megfelel a csúszásmentes gördülés feltételének, vagyis tekinthető a kis kerék kezdetben

A

-ban levő kerületi pontjának a kerék elfordulása utáni helyzetben.

Megjegyzés. Ha a gördülés egyenletes, vagyis

φ = ω t

, akkor

\begin{matrix} O M = 2 R cos φ = 2 R cos ω t, \end{matrix}

tehát

M

mozgása

2 R

amplitúdójú, a kerék gördülésével azonos periódusidejű harmonikus rezgőmozgás.

Markó Péter (Győr, Révai Miklós Gimn., 10. évf.)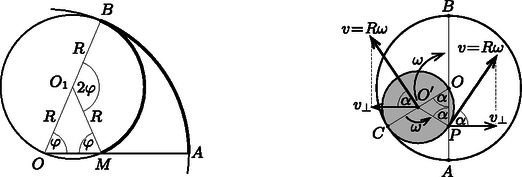

\begin{matrix} 1. ábra \end{matrix}

\begin{matrix} 2. ábra \end{matrix}

[htb

II. megoldás. Tekintsük az

R

sugarú gördülő kerék tetszőleges helyzetét (2. ábra). A kerék kerületének kiszemelt

P

pontja és a nagy kör

O

középpontja kijelöli a

2 R

sugarú kör

A B

átmérőjét. Megmutatjuk, hogy a kerék gördülése során a

P

pont nem távolodik el az

A B

egyenestől, mindvégig rajta marad azon.
A kerék mozgása két részből tehető össze. Egyrészt az

O'

középpontja valamekkora

ω

szögsebességgel elfordul a nagy kör

O

középpontja körül; ebből a mozgásból származó sebessége

v = R ω

. Másrészt a kerék ugyancsak

ω

szögsebességgel, de az ellenkező irányban forog a saját

(O')

középpontja körül; a kerületi pontjainak, így

P

-nek is az ebből származó sebessége

R ω

Megjegyzés. A kétféle mozgás szögsebességének egyenlő nagyságát jól mutatja az tény, hogy a kerék

C

pontjának eredő sebessége ‐ a csúszásmentes gördülés miatt ‐ nulla. A kerék

C

pontja (ami tényleges anyagi pont) nem tévesztendő össze a kerék és a nagy kör pillanatnyi érintkezési pontjával, amit mindig más és más anyagdarabkák jelölnek ki, és amelyik pont nem is mozdulatlan, hanem

ω' = ω / 2

szögsebességgel ,,jár körbe'' az

O

pont körül.

A kétféle mozgásból adódó sebességvektor nagysága és az

A B

átmérővel bezárt szöge ugyanakkora, emiatt az

A B

-re merőleges

v_{⊥}

sebességkomponensek is egyenlő nagyságúak (de ellentétes irányúak). Ezek szerint a

P

pont nem távolodik el az

A B

egyenestől, a kerék gördülése során mindvégig azon marad.

Tallósy Péter (Szeged, Dugonics András Piarista Gimn., 8. évf.)
dolgozata alapján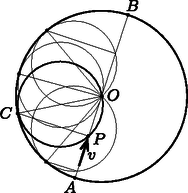

III. megoldás. Tekintsük a gördülő kerék valamelyik (a 3. ábrán vastagabban jelölt) helyzetét! A mozgás pillanatnyi forgási középpontja (ún. momentán centruma) a két kör érintkezési pontja, vagyis

C

, hiszen ezen pont sebessége nulla. A kerék kijelölt kerületi pontjának (

P

) sebessége merőleges

C P

-re, tehát átmegy a nagy kör

O

középpontján, hiszen a kis kerék határvonala az

C O P

háromszög Thalész-köre. Ezek szerint a

P

pont sebessége mindvégig az

O

középpont felé, vagy azzal ellentétes irányba mutat, a

P

pont pályája tehát a nagy kör egyik átmérője.

3. ábra

(G. P.)

Megjegyzés. Amikor egy

R_{1}

sugarú kör kerületének belső oldalán csúszásmentesen gördül körbe egy másik,

R_{2} < R_{1}

sugarú kör, akkor a belső kör egy pontja által leírt pályát hipocikloisnak nevezzük, aminek a pontjait ‐ alkalmasan választott koordináta-rendszerben ‐ a következőképpen számíthatjuk ki:

\begin{matrix} x (t) & = (R_{1} - R_{2}) cos t + R_{1} cos \frac{(R_{1} - R_{2}) t}{R_{2}}, \\ y (t) & = (R_{1} - R_{2}) sin t - R_{1} sin \frac{(R_{1} - R_{2}) t}{R_{2}} . \end{matrix}

Amennyiben

R_{1} = 2 R

és

R_{2} = R

, a hipociklois elfajult lesz,

y (t) \equiv 0

egyenletű egyenessé válik.
Bányai Kristóf (Miskolc, Herman Ottó Gimn., 9. évf.)