Feladat:	5066. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Elek Péter ,  Markó Gábor
Füzet:	2018/december, 567 - 570. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Egyéb fénytörés
Hivatkozás(ok):	Feladatok: 2018/október: 5066. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. 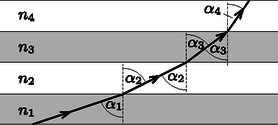  I. megoldás. Ha képzeletben vékony, egyre növekvő törésmutatójú átlátszó plánparalel (két párhuzamos síkkal határolt) lemezeket helyezünk egymásra, és rajtuk keresztül egy vékony fénysugár halad (1. ábra), akkor a Snelius‐Descartes-törvény szerint $\begin{array}{c}{\displaystyle \frac{\text{sin}{\alpha }_2}{\text{sin}{\alpha }_1}=\frac{n_1}{n_2}\mathrm{,}\frac{\text{sin}{\alpha }_3}{\text{sin}{\alpha }_2}=\frac{n_2}{n_3}\mathrm{,}\frac{\text{sin}{\alpha }_4}{\text{sin}{\alpha }_3}=\frac{n_3}{n_4}\text{...}\mathrm{,}}\end{array}$ azaz $\begin{array}{c}{\displaystyle n_1\text{sin}{\alpha }_1=n_2\text{sin}{\alpha }_2=n_3\text{sin}{\alpha }_3=\text{...}=\text{állandó}\mathrm{,}}\end{array}$ (1) tehát a beesési szög szinusza és az abszolút törésmutató szorzata a helytől függetlenül állandó. A folyamatosan változó törésmutatójú közegre is érvényes ez az összefüggés, hiszen a közeget tekinthetjük úgy, mintha vékony plánparalel lemezekből épülne fel.   1. ábra   Helyezzük a koordináta-rendszer origóját a fénysugár kiindulási pontjához. A feladat szövege szerint a $z$ tengely irányára merőlegesen, az $x$ tengely irányában indítjuk a vékony fénysugarat (2. ábra). Az origóban (a parabola csúcspontjában) a beesési szög ${90}^{\circ }$-os, így az (1)-ben szereplő állandó $n_0$. A törésmutató egy tetszőleges $z$ koordinátával megadott $P$ pontban   $\begin{array}{c}{\displaystyle n\left(z\right)=\frac{n_0}{\text{sin}\alpha \left(z\right)}\mathrm{,}}\end{array}$ ahol $\alpha \left(z\right)$ a parabola $P$ pontbeli érintőjének a $z$ tengellyel bezárt szöge (vagyis az elgörbülő fénysugár ottani ,,beesési szöge''). Azt is tudjuk, hogy $z=h$-nál a törésmutató $\sqrt[]{2}{n}_0$, vagyis ezen a helyen $\te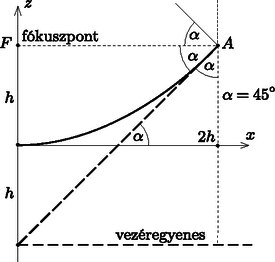xt{sin}\alpha \left(h\right)=1/\sqrt[]{2}$, tehát $\alpha \left(h\right)={45}^{\circ }$.   2. ábra   A parabola ismert tulajdonsága, hogy az érintője felezi azt a szöget, amelyet az érintési pontból a vezéregyenesre emelt merőleges és az érintési pontból a fókusz felé indított félegyenes bezár (lásd pl. Reiman István Matematika, Typotex (2014), https://www.tankonyvtar.hu/hu/tartalom/tamop425/2011-0001-526_ reimann_matematika/ch17s04.html). (A parabola ezen tulajdonsága tesz lehetővé számos műszaki alkalmazást, pl. a parabolatükrök, fényszórók és antennák működését.) Alkalmazzuk az érintő irányára vonatkozó ismeretet a parabola $z=h$ ,,magasan'' lévő $A$ pontjára, ebből megkapjuk, hogy az $F$ fókuszpont, valamint a vezéregyenes a csúcsponttól $h$ távolságra van, és a parabola egyenlete: 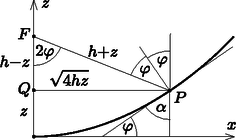$\begin{array}{c}{\displaystyle z\left(x\right)=\frac{x^2}{4h}\mathrm{,}\text{azaz}x\left(z\right)=\sqrt[]{4hz}\mathrm{.}}\end{array}$ (2)   3. ábra   Határozzuk meg a fénysugár parabola pályájának tetszőleges $P$ pontjában az érintő és az $x$ tengely $\phi ={90}^{\circ }-\alpha$ szögét (3. ábra), majd annak ismeretében olvassuk le a törésmutató $n\left(z\right)$ függvényének alakját. A $P$ pont az $x$ tengelytől $z$, a vezéregyenestól $h+z$ távol van, így a fókuszponttól mért távolsága is $h+z$. Másrészt $FQ=h-z$, tehát $\begin{array}{c}{\displaystyle \text{cos}\left(2\phi \right)=\frac{h-z}{h+z}\mathrm{,}\text{így}\text{cos}\phi =\sqrt[]{\frac{1+\text{cos}\left(2\phi \right)}{2}}=\sqrt[]{\frac{h}{h+z}}\mathrm{,}}\end{array}$ a keresett törésmutató pedig $\begin{array}{c}{\displaystyle n\left(z\right)=\frac{n_0}{\text{sin}\alpha \left(z\right)}=\frac{n_0}{\text{cos}\phi \left(z\right)}=n_0\sqrt[]{1+\frac{z}{h}}\mathrm{.}}\end{array}$    Markó Gábor (Győr, Révai Miklós Gimn., 12. évf.)     II. megoldás. A fény terjedését változó törésmutatójú közegben nemcsak a sok-sok vékony rétegre felírt Snelius‐Descartes-törvénnyel, hanem a Fermat-elv segítségével is le lehet írni. Ez utóbbi azt állítja, hogy helyről helyre változó $n\left(\text{<span style="font-weight: bold;"><span style="font-style: italic;">r</span></span>}\right)$ törésmutató esetén egy vékony fénysugár ,,mozgása'' olyan pálya mentén megy végbe, amelyre az adott kezdő- és végpont közötti terjedés ideje, vagyis a   $\begin{array}{c}{\displaystyle T=\frac{1}{c}\int n\left(\text{<span style="font-weight: bold;"><span style="font-style: italic;">r</span></span>}\right)\text{d}s}\end{array}$ integrál értéke a lehető legkisebb. (Az integrálás a pályagörbe $s$-sel jelölt ívhossza szerint történik.) A szokásos kérdésfeltevés az, hogy adott módon változó törésmutatóhoz milyen ,,fénypályagörbe'' tartozik. Jelen esetben azonban a megfordított kérdésre keressük a választ: Milyen módon változó törésmutató eredményez egy megadott pálya (parabolaív) mentén történő fényterjedést? Hasonló minimumelv a klasszikus mechanikai mozgásokra is megfogalmazható (lásd pl. Solt György: Variációs elvek a klasszikus és kvantumfizikában c. cikket lapunk 490. oldalán. ‐ a Szerk.). A Maupertuis-elv szerint egy adott összenergiájú, pontszerű test a tér két adott pontja között olyan pályán mozog, amelyre a   $\begin{array}{c}{\displaystyle W=\int v\left(\text{<span style="font-weight: bold;"><span style="font-style: italic;">r</span></span>}\right)\text{d}s}\end{array}$   integrál minimális, ahol $v\left(\text{<span style="font-weight: bold;"><span style="font-style: italic;">r</span></span>}\right)$ a test sebességének ‐ általában helyről helyre változó ‐ nagysága. Ebben az esetben is az a szokásos kérdés, hogy adott módon változó (például az energiamegmaradás tételéből kiszámítható) sebességnagyság esetén milyen a pályagörbe alakja, de itt is feltehető a megfordított kérdés: Milyen módon változzon a test sebességének nagysága, hogy a mozgás pályagörbéje adott alakú (mondjuk parabolaív) legyen? Természetes módon kínálkozik az a gondolat, hogy a Fermat-elv és a Maupertuis-elv közötti hasonlóságot kihasználjuk. Ha ismerjük az egyik (a mechanikai) probléma megoldását, abból következtethetünk a másik (az optikai) feladat megoldására. Jelen esetben az $x$ tengely mentén elinduló és csak a $z$ koordinátától függő $n\left(z\right)$ törésmutatójú közegben haladó fénysugárnak egy olyan mechanikai mozgás felel meg, amelyben a kezdősebesség (egy alkalmasan választott koordináta-rendszerben) vízszintes irányú, és a sebesség nagysága csak a másik koordinátától ($z$-től) függ (tehát a test függőleges irányú erőtérben mozog). Tudjuk, hogy a mozgás pályagörbéje akkor lesz parabola, ha az erőtér homogén, vagyis a vízszintes hajítás jól ismert esetével van dolgunk. Egy $v_0$ kezdősebességgel eldobott test sebességének nagysága (függőlegesen lefelé irányított $z$ tengely mellett) $v\left(z\right)=\sqrt[]{v_0^2+2gz}$. Az analóg optikai feladat megoldása eszerint $n\left(z\right)=c_1\sqrt[]{1+c_{2}z}$, ahol $c_1$ és $c_2$ alkalmasan választott állandók. Mivel ismerjük, hogy $n\left(0\right)=n_0$ és $n\left(h\right)=\sqrt[]{2}{n}_0$, ezekből $c_1=n_0$ és $c_2=1/h$ következik, vagyis a törésmutató $z$-függése: $\begin{array}{c}{\displaystyle n\left(z\right)=n_0\sqrt[]{1+\frac{z}{h}}\mathrm{.}}\end{array}$    Elek Péter (Debreceni Ref. Koll. Dóczy Gimn., 12. évf.)  dolgozata alapján