Feladat:	5006. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bartók Imre ,  Csire Roland ,  Csuha Boglárka ,  Elek Péter ,  Fajszi Bulcsú ,  Fekete Balázs Attila ,  Kolontári Péter ,  Marozsák Tóbiás ,  Olosz Adél ,  Póta Balázs
Füzet:	2018/október, 436 - 438. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Tömegközéppont mozgása
Hivatkozás(ok):	Feladatok: 2018/február: 5006. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. $a)$ A labda legjobban benyomódott állapotában $\begin{array}{c}{\displaystyle A={\left(5\text{cm}\right)}^2\pi =7\mathrm{,}85\cdot {10}^{-3}{\text{m}}^2}\end{array}$ területű körlap mentén érintkezik a talajjal. Legyen a labda teljes tömege $m$, a talajjal érintkező részének tömege $m^{*}$. A külső légnyomást jelöljük $p_0$-lal, a labdában lévő levegő legnagyobb nyomását pedig $p_1$-gyel (1. ábra). $a)$ A labda benyomódott részére felülről $p_{1}A$ erő hat, alulról pedig (amennyiben a labda alatt levegő marad) $p_{0}A+K_1$ erő nyomja felfelé. $K_1$ a göröngyös talaj által kifejtett kényszererőt jelöli. A labda többi része ,,simán'', vízszintesen csatlakozik a körlap alakú részhez, így nem fejthet ki arra eredő függőleges erőt. A körlap az ütközés ideje alatt nem gyorsul, hiszen az bizonyos ideig folyamatosan a talajjal érintkezik, így a mozgásegyenlete: $\begin{array}{c}{\displaystyle m^{*}g+p_{1}A=p_{0}A+K_1\mathrm{,}\text{vagyis}{K}_1=\left(p_1-p_0\right)A+m^{*}g\mathrm{.}}\end{array}$   Megjegyzés: Mivel a nyomáskülönbségből származó első tag kb. 78 N, a körlapra ható nehézségi erő pedig biztosan kisebb, mint $mg=2$ N, jó közelítéssel igaz, hogy 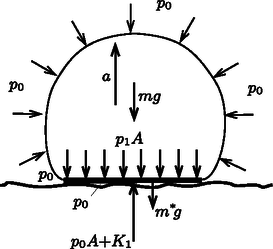$\begin{array}{c}{\displaystyle K_1\approx \left(p_1-p_0\right)A\mathrm{.}}\end{array}$     1. ábra 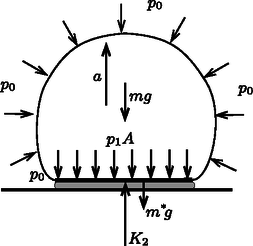      2. ábra   Vizsgáljuk most meg a labda többi részére ható külső erőket! A légnyomás által kifejtett erő $p_{0}A$ nagyságú, és függőlegesen lefelé mutat, hiszen a légnyomásból származó erők eredője a teljes labdára nulla, és a talajjal érintkező körlapra a külső levegő $p_{0}A$ nagyságú, függőlegesen felfelé mutató erőt fejt ki. A labda egészére felírható mozgásegyenlet (a függőlegesen felfelé mutató irányt tekintve pozitívnak): $\begin{array}{c}{\displaystyle K_1+p_{0}A-mg-p_{0}A=ma\mathrm{,}}\end{array}$ ahonnan $K_1$ korábban kiszámított értékének behelyettesítése után a tömegközéppont gyorsulása: $\begin{array}{c}{\displaystyle a=\frac{\left(p_1-p_0\right)A}{m}-\frac{m-m^{*}}{m}g\approx \frac{\left(p_1-p_0\right)A}{m}-g\approx 380\frac{\text{m}}{{\text{s}}^2}\mathrm{.}}\end{array}$   $b)$ Ha a talaj felülete sima és nedves, akkor a labda alatt nem marad levegő, tehát a légnyomásból származó $p_{0}A$ erő most nem lép fel. Helyette viszont a vízréteg és a talaj fejt ki a labda aljára valamekkora erőt. (A talajon lévő víz a labdán kívül is jelen van, és ott érintkezik a külső levegővel, így a nyomása gyakorlatilag $p_0$. Ha viszont a labda ténylegesen lezárja az alája szorult vizet, akkor a víz nyomása akár $p_1$ is lehet.) A talajjal érintkező labdadarab nem gyorsul, így a mozgásegyenlete: $\begin{array}{c}{\displaystyle m^{*}g+p_{1}A=K_2\mathrm{,}}\end{array}$ ahol $K_2$ a talaj és a vízhártya által kifejtett eredő erő (2. ábra). Az ábrán ‐ az egyszerűség kedvéért ‐ nem jelöltük, hogy a labda alja milyen mértékben érintkezik közvetlenül a talajjal, illetve a vízzel. A labda egészének mozgásegyenlete: $\begin{array}{c}{\displaystyle K_2-mg-p_{0}A=ma\mathrm{,}}\end{array}$ vagyis a tömegközéppont gyorsulása: $\begin{array}{c}{\displaystyle a=\frac{\left(p_1-p_0\right)A}{m}-\frac{m-m^{*}}{m}g\approx 380\frac{\text{m}}{{\text{s}}^2}\mathrm{.}}\end{array}$ Ez az érték ugyanakkora, mint az $a)$ esetben volt a tömegközéppont gyorsulása.   II. megoldás. Használjuk az I. megoldás jelöléseit! A labda lendülete a legjobban benyomódott állapotban és az azt megelőző, illetve követő pillanatokban így írható fel: $\begin{array}{c}{\displaystyle I^{\text{teljes}}\left(t\right)=I^{\text{felső}}\left(t\right)+I^{\text{alsó}}\left(t\right)\equiv I^{\text{felső}}\left(t\right)\mathrm{,}}\end{array}$ hiszen az alsó rész az ütközés alatt folyamatosan nyugalomban van, tehát ezalatt a lendülete nulla. (Az ,,alsó'' kifejezés a labdának a talajjal érintkező részére, a ,,felső'' pedig a többi részre utal.) Newton II. törvényét ilyen alakban is felírhatjuk: $\begin{array}{c}{\displaystyle ma=\frac{\Delta I^{\text{teljes}}\left(t\right)}{\Delta t}=\frac{\Delta I^{\text{felső}}\left(t\right)}{\Delta t}=F^{\text{felső}}\mathrm{,}}\end{array}$ ahol $\begin{array}{c}{\displaystyle F^{\text{felső}}=p_{1}A-p_{0}A-\left(m-m^{*}\right)g}\end{array}$ a felső részre ható erők (a külső és a belső légnyomásból származó erők és a nehézségi erő) eredője. Az eredő erő képletében szereplő első két tag nagyságát onnan kaphatjuk meg, hogy tudjuk: egy teljes, zárt felületre ható, a légnyomásból származó erők eredője nulla. A fenti összefüggés felírásánál kihasználtuk, hogy a hajlékony anyagú labda alsó része nem fejthet ki függőleges irányú erőt a felső részre, mert a két rész vízszintes érintősíkkal, ,,törésmentesen'' csatlakozik egymáshoz. A fenti egyenletekből a tömegközéppont gyorsulására $\begin{array}{c}{\displaystyle a=\frac{\left(p_1-p_0\right)A}{m}-\frac{m-m^{*}}{m}g\approx 380\frac{\text{m}}{{\text{s}}^2}}\end{array}$ adódik. Ez az eredmény független attól, hogy a labda alsó része és a talaj között milyen a kapcsolat, vagyis hogy a talaj száraz-e vagy nedves, sima-e vagy pedig göröngyös.    (G. P.)