|
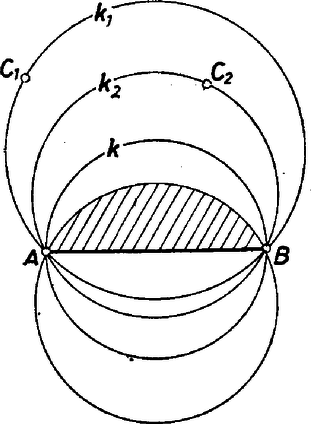
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Legyen az adott pontok száma. Válasszunk ki közülük kettőt, amelyeknek a távolsága a legkisebb. Ilyen biztosan van, mert csak véges sok pontunk van, ha több ilyen pontpárunk is van, akkor ezek egyikét. Jelöljük a pontokat -val és -vel. Az fölé mint átmérő fölé rajzolt kör nem tartalmaz a belsejében egyet sem az adott pontok közül, mert különben lenne 2 pont, amelyeknek a távolsága kisebb lenne az távolságnál. Ha most olyan kört rajzolunk, amelynek húrja, akkor ennek a körnek az által levágott kisebbik szeletében biztosan nincs egyetlen pont sem az adottak közül, hiszen ez a körszelet teljesen -ban van. Most válasszunk egyet a maradék pontok közül (ilyen van, mert ), legyen ez , és rajzoljuk meg az pontokon átmenő kört. Ha belsejében nincsen pont, akkor készen vagyunk, hiszen átmegy három adott ponton. Ha van, legyen ez a , és rajzoljuk meg az kört, -t. -ben kevesebb pont van az adottak közül , mint -ben, mert az által levágott kisebbik szeletében ugyanúgy nincs adott pont, mint esetében, a nagyobb szelet, pedig része -nek. Az eljárást ismételve legfeljebb az -edik lépésben megtaláljuk azt a kört, amely már egyet sem tartalmaz a belsejében az adott pontok közül. |
 PDF |
PDF |  MathML
MathML