Kezdőlap


Feladat:	B.4910	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Csizmadia Viktória
Füzet:	2018/május, 285 - 286. oldal		PDF \| MathML
Témakör(ök):	Feladat, Síkgeometriai bizonyítások, Háromszögek hasonlósága, Másodfokú (és arra visszavezethető) egyenletek, Pont körüli forgatás
Hivatkozás(ok):	Feladatok: 2017/november: B.4910

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Tudjuk, hogy $X = X'$ . Legyen a négyzet oldala egységnyi, ez nem jelent korlátozást. Legyen 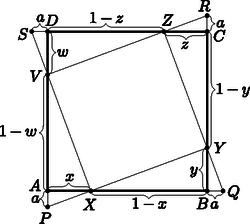$A P = B Q = C R = D S = a$ , továbbá $A X = x$ , $X B = 1 - x$ , $B Y = y$ , $Y C = 1 - y$ , $C Z = z$ , $Z D = 1 - z$ , $D V = w$ és $V A = 1 - w$ .

Ekkor a

D V Z

háromszög hasonló lesz a

C R Z

háromszöghöz, mivel a

D V

oldal párhuzamos a

C R

oldallal, a másik két oldaluk pedig egy egyenesre esik. Megfelelő oldalaik aránya tehát megegyezik:

\begin{matrix} \frac{z}{1 - z} = \frac{a}{w} . \end{matrix}

Ugyanígy az

S D V

és az

X A V

háromszögek is hasonlóak lesznek, tehát a megfelelő oldalaik aránya megegyezik:

\begin{matrix} \frac{a}{w} = \frac{x}{1 - w} . \end{matrix}

Ebből a két egyenletből következik, hogy

\begin{matrix} \frac{z}{1 - z} = \frac{x}{1 - w} . \end{matrix}

Ugyanígy felírva a

P A X

és

X B Y

, illetve

Q B Y

és

Z C Y

hasonló háromszögekre az arányokat kapjuk, hogy

\begin{matrix} \frac{a}{x} = \frac{y}{1 - x} \Leftrightarrow \frac{x}{1 - x} = \frac{a}{y} és \frac{a}{y} = \frac{z}{1 - y} . \end{matrix}

Ezzel tehát az is teljesül, hogy

\begin{matrix} \frac{z}{1 - y} = \frac{x}{1 - x} . \end{matrix}

Osszuk el egymással a

\frac{z}{1 - z} = \frac{x}{1 - w}

és

\frac{z}{1 - y} = \frac{x}{1 - x}

egyenletek megfelelő oldalait. Kapjuk, hogy

\begin{matrix} \frac{1 - y}{1 - z} = \frac{1 - x}{1 - w} . \end{matrix}

(1)

Az oldalak betűzésétől függetlenül jöttek ki ezek az arányok, így ugyanezek miatt felírható az is, hogy:

\begin{matrix} \frac{1 - z}{1 - w} = \frac{1 - x}{1 - y} . \end{matrix}

Ebből átrendezéssel:

\begin{matrix} \frac{1 - y}{1 - w} = \frac{1 - x}{1 - z} . \end{matrix}

(2)

Az (1) és (2) hányadosára:

\begin{matrix} \frac{1 - w}{1 - z} = \frac{1 - z}{1 - w} . \end{matrix}

Ez pedig csak úgy lehet, ha

\begin{matrix} 1 - w = 1 - z . \end{matrix}

Szimmetria miatt

1 - y = 1 - x = 1 - w = 1 - z

is igaz lesz. Ez pedig azt jelenti, hogy az

A B C D

négyzet oldalait egyenlő arányban osztják az

X Y Z V

négyszög csúcsai, tehát az

X B Y

Y C Z

Z D V

és

V A X

háromszögek egybevágó derékszögű háromszögek. Ebből pedig már következik, hogy

X Y Z V

négyzet (mivel oldalai egyenlő hosszúak és merőlegesek egymásra), és éppen ezt akartuk belátni.

Csizmadia Viktória (Budapesti Fazekas M. Gyak. Ált. Isk. és Gimn., 11. évf.)
dolgozata alapján