| Feladat: | B.4918 | Korcsoport: 16-17 | Nehézségi fok: nehéz |
| Megoldó(k): | Zsigri Bálint | ||
| Füzet: | 2018/április, 223 - 224. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Feladat, Térgeometriai bizonyítások, Vektorok | ||
| Hivatkozás(ok): | Feladatok: 2017/december: B.4918 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Az adott egységvektorok legyenek , az origó középpontú egységnyi sugarú gömböt jelölje . Legyen az a pont, aminek helyvektora ; továbbá a középpontú egységgömböt jelölje . 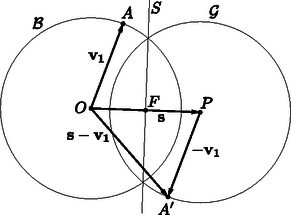 Vetítsük le a vektorokat az egyenesre, és tekintsük a vetületek előjeles hosszát: ha a vetületvektor -sel egyállású, akkor a hosszát pozitívnak tekintjük, egyébként negatívnak. Mivel a vektorok összege éppen , azért a vetületek előjeles hosszának összege . Így van olyan vektor, mondjuk , amely vetületének előjeles hossza legfeljebb . Ez geometriailag pontosan azt jelenti, hogy az origóból egy olyan pontba mutat, amely az -nek az origót tartalmazó zárt félterébe esik. Messük el a és gömböket az síkkal, így kapjuk az ábrát. Legyen az pontnak az szakasz felezőpontjára vett tükörképe . Ekkor , ezért , azaz darab adott vektor összege. A tükrözés miatt az sík elválasztja az és pontokat (esetleg ), valamint illeszkedik felszínére, ezért ‐ ahogyan az az ábráról leolvasható ‐ nem lehet a gömb belsejében. Így , és a bizonyítást befejeztük. Zsigri Bálint (Budapest, Szent István Gimn., 11. évf.) |