Kezdőlap


Feladat:	B.4906	Korcsoport: 14-15	Nehézségi fok: nehéz
Megoldó(k):	Győrffy Ágoston , Lukács Lilla Réka , Olosz Adél , Schrettner Jakab
Füzet:	2018/április, 219 - 221. oldal		PDF \| MathML
Témakör(ök):	Feladat, Háromszög területe, Középvonal, Természetes számok
Hivatkozás(ok):	Feladatok: 2017/november: B.4906

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Használjuk az 1. ábrát. Legyenek az $A B E$ , $A E F$ , $A F D$ , $F E C$ háromszögek területeinek mérőszámai (nem feltétlenül ebben a sorrendben) az $n$ , $n + 1$ , $n + 2$ , $n + 3$ pozitív egész számok. Ekkor $T_{A B C D} = 4 n + 6$ . Mivel $T_{A B C D} = T_{A B D} + T_{B C D}$ , emiatt $T_{A B D}$ pontosan akkor maximális, ha $T_{B C D}$ minimális.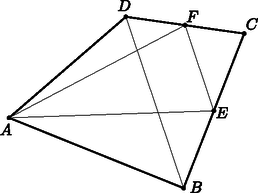

1. ábra

Másfelől a

B C D

háromszögben

E F

B D

-vel párhuzamos középvonal, emiatt a

B C D

háromszög hasonló az

E C F

háromszöghöz. A hasonlóság aránya 2, így a háromszögek területeire

T_{B C D} = 4 \cdot T_{E C F}

teljesül.
Mivel

T_{E C F}

n

n + 1

n + 2

n + 3

számokból kerül ki, ezért

T_{B C D}

akkor a legkisebb, ha

T_{E C F} = n

, és ekkor

T_{B C D} = 4 \cdot T_{E C F} = 4 n

. Ekkor

T_{A B D} = T_{A B C D} - T_{B C D} = (4 n + 6) - 4 n = 6

.
Vagyis az

A B D

háromszög területének lehető legnagyobb értéke

6

területegység.
Meg kell még mutatnunk, hogy létezik megfelelő

A B C D

négyszög. Ehhez néhány példa a beküldött jó konstrukciók közül. (Sajnos a beküldött megoldások jelentős részében ezt elfelejtették megmutatni, ezért a viszonylag sok

4

pontos dolgozat.)
1. példa: Legyen

A B C D

olyan trapéz, melynek alapjai

A B = 6

, illetve

C D = 4

és az alapokhoz tartozó magassága

2

(2. ábra). Ekkor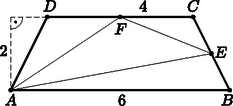

T_{A B D} = 6

;

T_{A B C D} = 10

T_{A B E} = 3

T_{A F D} = 2

és

T_{E C F} = 1

, amiből

T_{A E F} = 10 - (3 + 2 + 1) = 4

2. ábra

2. példa: Most

A B C D

olyan trapéz, melynek alapjai

B C = 4

, illetve

A D = 3

és az alapokhoz tartozó magassága

3

(3. ábra). Ekkor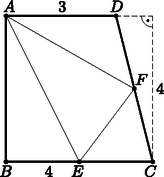

T_{A B D} = 6

;

T_{A B C D} = 14

T_{A B E} = 4

T_{A F D} = 3

és

T_{E C F} = 2

, amiből

T_{A E F} = 14 - (4 + 3 + 2) = 5

3. ábra

(Több példa voltaképpen ezen a két ábrán alapult; az alapokat felezve, kétszerezve, vagy

\sqrt[]{2}

-vel osztva, míg a magasságot pont fordítva alakítva: duplázva, felezve, illetve

\sqrt[]{2}

-vel szorozva.)
3. példa: Az utolsó példánk (bár

A B

itt is párhuzamos

C D

-vel) arra épít, hogy a négyszög átlói merőlegesek egymásra. Legyen

A B C D

olyan négyszög, melynek átlói merőlegesen metszik egymást az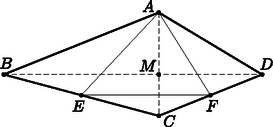

M

pontban,

\begin{matrix} A M = \frac{6 \sqrt[]{2}}{5}, C M = \frac{4 \sqrt[]{2}}{5}, B M = 3 \sqrt[]{2} és D M = 2 \sqrt[]{2} \end{matrix}

hosszú (4. ábra). Ekkor

\begin{matrix} T_{A B E} & = \frac{T_{A B C}}{2} = \frac{3 \sqrt[]{2} \cdot (\frac{6 \sqrt[]{2}}{5} + \frac{4 \sqrt[]{2}}{5})}{2 \cdot 2} = 3, \\ T_{A F D} & = \frac{T_{A C D}}{2} = \frac{2 \sqrt[]{2} \cdot (\frac{6 \sqrt[]{2}}{5} + \frac{4 \sqrt[]{2}}{5})}{2 \cdot 2} = 2, \\ míg \\ T_{E C F} & = \frac{T_{B C D}}{4} = \frac{(2 \sqrt[]{2} + 3 \sqrt[]{2}) \cdot \frac{4 \sqrt[]{2}}{5}}{2 \cdot 4} = 1. \end{matrix}

Mivel

\begin{matrix} T_{A B C D} = \frac{A C \cdot B D}{2} = \frac{5 \sqrt[]{2} \cdot \frac{10 \sqrt[]{2}}{5}}{2} = 10, innen T_{A E F} = 10 - (3 + 2 + 1) = 4. \end{matrix}

Végül

\begin{matrix} T_{A B D} = \frac{(2 \sqrt[]{2} + 3 \sqrt[]{2}) \cdot \frac{6 \sqrt[]{2}}{5}}{2} = 6. \end{matrix}

4. ábra

Győrffy Ágoston (Budapesti Fazekas M. Gyak. Ált. Isk. és Gimn., 11. évf.)
Lukács Lilla Réka (Budapest, Szent István Gimn., 11. évf.),
Olosz Adél (Pécs, PTE Gyak. Ált. Isk., Gimn. és Szakgimn., 11. évf.) és
Schrettner Jakab (Szegedi Radnóti Miklós Kís. Gimn., 11. évf.)
dolgozata alapján