Kezdőlap


Feladat:	B.4884	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Baran Zsuzsanna , Daróczi Sándor , Döbröntei Dávid Bence , Fülöp Anna Tácia , Gáspár Attila , Győrffy Ágoston , Imolay András , Kerekes Anna , Kővári Péter Viktor , Lakatos Ádám , Scheidler Barnabás , Sulán Ádám , Szabó Dávid , Tiderenczl Dániel , Tóth Viktor , Weisz Máté
Füzet:	2018/április, 215 - 217. oldal		PDF \| MathML
Témakör(ök):	Feladat, Háromszög területe, Négyzetek
Hivatkozás(ok):	Feladatok: 2017/május: B.4884

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A minimális területű háromszög minden oldala biztosan tartalmazza a négyzetnek legalább egy pontját, különben a megfelelő oldalegyenest a négyzet irányába párhuzamosan eltolhatnánk, amivel a háromszög területét csökkentenénk. Világos, hogy ha a háromszög egyik oldala tartalmazza a négyzet egy oldalának egy belső pontját, akkor az egész oldalt is tartalmazza (mivel a háromszög tartalmazza a négyzetet), ezért feltehetjük, hogy a minimális területű háromszög minden oldala biztosan tartalmazza a négyzetnek legalább egy csúcsát. Ha két oldal ugyanazt a négyzetcsúcsot tartalmazza, akkor a háromszögnek és négyzetnek van egy közös csúcsa. E közös csúcs körül a háromszög illeszkedő oldalait elforgathatjuk, hogy rendre egybeessenek a négyzet oldalaival, ezzel a háromszög területét nem növeljük.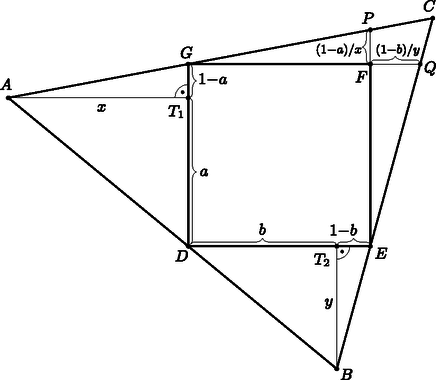

Összességében azt kaptuk, hogy az ábra általános érvényű azzal a kiegészítéssel, hogy a

C P F Q

négyszög esetleg szakasszá vagy ponttá fajulhat (s ezzel együtt az

A T_{1} G

és

B T_{2} E

háromszögek is elfajulhatnak természetesen), ezek azonban gondolatmenetünket érdemben nem befolyásolják. Használjuk tehát az ábra jelöléseit, továbbá legyen

D T_{1} = a

A T_{1} = x

;

D T_{2} = b

és

B T_{2} = y

. Ekkor

G T_{1} = 1 - a

és

E T_{2} = 1 - b

. A szögeik egyenlősége miatt

A T_{1} G ▵ \sim G F P ▵

és

B T_{2} E ▵ \sim E F Q ▵

teljesül, amiből

P F = (1 - a) / x

és

F Q = (1 - b) / y

adódik. Továbbá

\begin{matrix} A D T_{1} ▵ \sim D B T_{2} ▵ \end{matrix}

miatt

a b = x y

is teljesül. Az általánosság megszorítása nélkül feltehető, hogy

x / a \leq 1

. (Különben

y / b \leq 1

, és a szerepek szimmetrikusak.)
Becsüljük alulról az

A B C

háromszög

T

területét:

\begin{matrix} T & \geq T - T_{F Q C P} = T_{D E F G} + T_{A D G} + T_{B E D} + T_{F P G} + T_{Q F E} = & (1) \\ = 1 + \frac{x}{2} + \frac{y}{2} + \frac{\frac{1 - a}{x}}{2} + \frac{\frac{1 - b}{y}}{2} = 1 + \frac{x + y + \frac{1 - a}{x} + \frac{1 - b}{y}}{2} . \end{matrix}

Vegyük észre, hogy

\begin{matrix} \frac{1 - a}{x} + \frac{1 - b}{y} - \frac{1 - x y}{y} = \frac{1}{x} - \frac{a}{x} + \frac{1}{y} - \frac{1}{y} - \frac{b}{y} + x = x + \frac{1}{x} - (\frac{a}{x} + \frac{x}{a}) \geq 0, \end{matrix}

ugyanis a feltevés szerint

a \leq 1

, s így

x \leq \frac{x}{a} \leq 1

teljesül, továbbá az

f (t) = t + 1 / t

függvény a

(0,1]

intervallumon monoton csökken. Ebből, folytatva (1)-et, tovább becsülhetjük alulról

T

-t:

\begin{matrix} T \geq 1 + \frac{x + y + \frac{1 - x y}{y}}{2} = 1 + \frac{y + \frac{1}{y}}{2} \geq 1 + \frac{2}{2} = 2. \end{matrix}

Egyenlőség csak akkor állhat, ha

T_{F Q C P} = 0

, azaz a négyzet egyik oldala illeszkedik a háromszög valamely oldalára (a négyzet maradék két csúcsa pedig a háromszög másik két oldalán van). Egyszerű számolással meggyőződhetünk róla, hogy ilyenkor valóban

T = 2

.
Tehát egy egységnégyzetet magában foglaló háromszög területe legalább

2

területegység.

Daróczi Sándor (Nyíregyháza, Krúdy Gyula Gimn., 11. évf.)