| Feladat: | B.4820 | Korcsoport: 16-17 | Nehézségi fok: nehéz |
| Megoldó(k): | Andó Angelika , Baran Zsuzsanna , Beke Csongor , Borbényi Márton , Deák Bence , Gáspár Attila , Győrffy Ágoston , Imolay András , Kerekes Anna , Kocsis Júlia , Kovács Benedek , Kővári Péter Viktor , Márton Dénes , Matolcsi Dávid , Pap Benedek , Simon Dániel Gábor , Szabó Kristóf , Szakály Marcell , Szemerédi Levente , Tiderenczl Dániel , Tóth Viktor , Vankó Miléna , Várkonyi Dorka , Zólomy Kristóf | ||
| Füzet: | 2018/április, 211 - 213. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Feladat, Konstruktív megoldási módszer, Hossz, kerület, Terület, felszín | ||
| Hivatkozás(ok): | Feladatok: 2016/október: B.4820 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Bontsuk esetekre a feladatot aszerint, hogy egy paralelogramma hány oldala illeszkedik rácsvonalra. 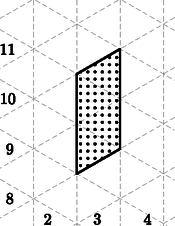 1. ábra 2. eset: Két oldal (nevezzük őket alapoknak) illeszkedik rácsvonalra. Mivel a paralelogramma magassága minimum (hiszen két párhuzamos rácsvonal között legalább ekkora a távolság), ezért az alapok hossza csak vagy lehet. 2.a eset: Az alapok hossza 2. Vegyük észre, hogy ha egy paralelogrammát ,,eltolunk'' egy egységgel (például a 2. ábrán a pontozottat a simába), akkor nem változik a belső rácsvonalak összege (hiszen a ,,leeső'', és ,,bekerülő'' háromszögek egybevágóak, eltolhatók egymásba, és ugyanannyi bennük a rácsvonalak összege). Ez csak akkor nem igaz, ha a keletkező paralelogramma mindegyik oldala rácsegyenesre illeszkedik, hiszen ekkor ,,elvész'' az oldal a paralelogramma belsejéből, vagyis ebben az esetben 1-gyel csökken az összhossz (például a 2. ábrán a sima paralelogrammából a csillagosba való ,,eltolásnál''). 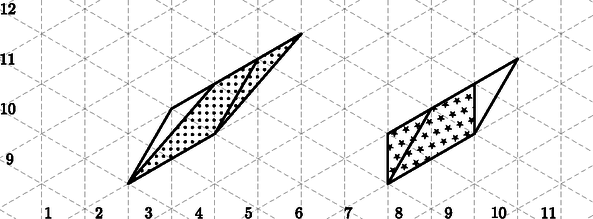 2. ábra Vagyis az összes ebbe az esetbe illő paralelogrammát eltolhatjuk egy teljesen rácsvonalakra illeszkedő paralelogrammába úgy, hogy közben 1-gyel csökken a belső rácsvonalak összege. Tehát ekkor a belső rácsvonalak összhossza. 2.b eset: Az alapok hossza 1 (3. ábra). 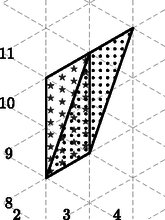 3. ábra Ekkor továbbra is igaz, hogy szabadon tologathatjuk a paralelogrammát, azonban a végén (amikor egy olyan paralelogrammát kapunk, amelynek minden oldala illeszkedik egy rácsegyenesre) a rácsvonalak összege -vel csökken. Vagyis ekkor a belső rácsvonalak összhossza. 3. eset: Nincs rácsvonalra illeszkedő oldala a paralelogrammának. Itt is igaz, hogy eltolhatjuk a paralelogrammát (nem feltétlenül egy egységgel), amíg egy olyat nem kapunk, amelynek az egyik oldala már rácsvonalra illeszkedik (4. ábra). 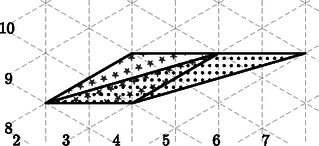 4. ábra Ekkor egy 2. esetbeli paralelogrammát kapunk (hiszen az eltolás nem változtat a paralelogramma területén), vagyis kétféle lehet: ‐ Ha az alapja , akkor az eltolás során -vel csökkent a belső rácsvonalak összhossza, vagyis kezdetben volt. ‐ Ha az alapja , akkor az eltolás során -gyel csökkent a belső rácsvonalak összhossza, vagyis kezdetben volt. Tehát ebben az esetben mindig a belső rácsvonalak összhossza Tehát egy területű paralelogrammában a rácsvonalak összhossza , , vagy lehet. Tóth Viktor (Kaposvári Táncsics Mihály Gimn., 12. évf.) |