Feladat:	2017. évi Eötvös fizikaverseny 3. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Füzet:	2018/március, 173 - 176. oldal		PDF  |  MathML
Témakör(ök):	Eötvös Loránd (korábban Károly Irén), Hővezetés, Becslési feladatok, Dimenzióanalízis
Hivatkozás(ok):	Feladatok: 2018/március: 2017. évi Eötvös fizikaverseny 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.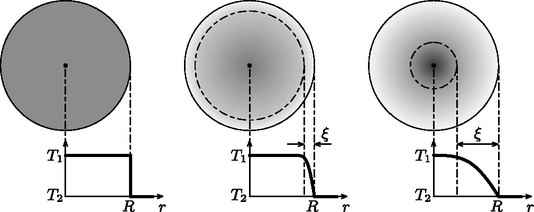   I. megoldás. A hosszú ideje lobogó vízbe merülő golyó belsejében a hőmérséklet mindenhol $T_1=100{}^{\circ }$C-os. Amikor a golyót a $T_2=0{}^{\circ }$C-os, jeges vízbe tesszük, akkor annak külső része kezd el először lehűlni, majd ez a ,,hidegfront'' halad fokozatosan a golyó belseje felé. A hőszigetelő edénybe helyezve a golyó belső energiája már nem változik tovább, csak annyi történik, hogy a hőmérséklet a belsejében kiegyenlítődik. Vajon mekkora tipikus $\xi$ mélységig hatol be a hidegfront a golyóba 30 másodperc alatt? Elképzelhető, hogy csak a golyó legkülső, vékony ,,kérge'' hűl le a jeges vízben, de az is, hogy szinte az egész golyó lehűl, csak a közepe táján marad meleg (4. ábra).   4. ábra   A golyó belseje és a jeges vízzel érintkező ($0{}^{\circ }$C-os) felülete közötti hővezetést a Fourier-törvény írja le, amely analóg a fémek elektromos vezetését leíró Ohm-törvénnyel (5. ábra). Míg egy állandó $A$ keresztmetszetű, $\Delta x$ hosszúságú egyenes vezetékben folyó elektromos áram ($I$) a vezeték végei közötti $\Delta U$ potenciálkülönbséggel arányos, addig ugyanezen vezetékben terjedő hőáram ($I_Q$) a $\Delta T$ hőmérséklet-különbséggel arányos: 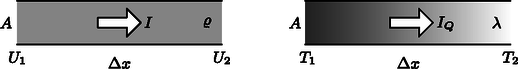$\begin{array}{c}{\displaystyle I=-\frac{1}{\varrho }A\frac{\Delta U}{\Delta x}\iff I_Q=-\lambda A\frac{\Delta T}{\Delta x}\mathrm{,}}\end{array}$ ahol $1/\varrho$ a vezeték anyagának elektromos vezetőképessége (a fajlagos ellenállás reciproka), $\lambda$ pedig a hővezetési tényező.   5. ábra   Sajnos golyó (gömbgeometria) esetén a Fourier-törvény matematikai alakja a fentinél bonyolultabb. További nehézség, hogy a feladatban a hőmérsékleteloszlás nem állandó (nem stacionárius), hanem a hőáram hatására időben változik. Ilyen körülmények között reménytelen a feladatra matematikailag egzakt választ adni. Megpróbálhatjuk azonban dimenzionális megfontolásokkal kitalálni, hogy hogyan függ a hidegfront $\xi$ behatolási mélysége az időtől. Első lépésként vizsgáljuk meg, milyen mennyiségektől függhet $\xi$. Természetesen függ az időtől, ezen kívül függ még a golyó $\lambda$ hővezetési tényezőjétől (rossz hővezető esetén $\xi$ lassabban növekszik), az üveg $\varrho$ sűrűségétől és $c$ fajhőjétől. A golyó $R$ sugara is fontos paraméter lehet, de ha $\xi \ll R$ (azaz a jeges vízbe merítés ideje viszonylag rövid), akkor a hidegfront terjedésére lényegében nincs hatással a golyó véges mérete. Mi a helyzet a golyó közepe és a felülete közötti hőmérséklet-különbséggel? A Fourier-törvény szerint kétszer akkora hőmérséklet-különbséghez kétszer akkora hőáram tartozik, de ekkor a golyó egyes rétegeinek lehűtéséhez szükséges hőelvonás is megkétszereződik. Tehát a hidegfront időbeli terjedését nem, csupán a ,,magasságát'' befolyásolja $\Delta T=T_1-T_2$ értéke. Keressük tehát a $\xi$ behatolási mélységet a következő alakban: $\begin{array}{c}{\displaystyle \xi \sim {\lambda }^{\alpha }{\varrho }^{\beta }{c}^{\gamma }{t}^{\delta }\mathrm{,}}\end{array}$ ahol $\alpha$, $\beta$, $\gamma$ és $\delta$ dimenziótlan konstans kitevők. A jobb oldalon álló mennyiségek mértékegységei: $\begin{array}{c}{\displaystyle \left[\lambda \right]=\frac{\text{<span style="font-weight: normal;font-style: normal;">kg</span>}\cdot \text{<span style="font-weight: normal;font-style: normal;">m</span>}}{{\text{<span style="font-weight: normal;font-style: normal;">s</span>}}^3\text{<span style="font-weight: normal;font-style: normal;">K</span>}}\mathrm{,}\left[\varrho \right]=\frac{\text{<span style="font-weight: normal;font-style: normal;">kg</span>}}{{\text{<span style="font-weight: normal;font-style: normal;">m</span>}}^3}\mathrm{,}\left[c\right]=\frac{{\text{<span style="font-weight: normal;font-style: normal;">m</span>}}^2}{{\text{<span style="font-weight: normal;font-style: normal;">s</span>}}^2\text{<span style="font-weight: normal;font-style: normal;">K</span>}}\mathrm{,}\left[t\right]=\text{<span style="font-weight: normal;font-style: normal;">s</span>}\mathrm{.}}\end{array}$ Ezekből csak egyféleképpen ,,keverhetünk ki'' méter dimenziójú mennyiséget: $\begin{array}{c}{\displaystyle \xi \left(t\right)\sim \sqrt[]{\frac{\lambda t}{c\varrho }}\mathrm{.}}\end{array}$ Egy dimenziótlan faktor erejéig most már ismerjük a $\xi \left(t\right)$ függvényt, de vajon mi az arányossági tényező? Nem tudjuk, de várhatóan egységnyi nagyságrendű, és mivel becslésről volt szó, vegyük 1-nek! A megadott adatok alapján tehát $t=30$ s alatt a ,,hidegfront'' behatolási mélysége: $\begin{array}{c}{\displaystyle \xi \approx \sqrt[]{\frac{\lambda t}{c\varrho }}\approx 3\mathrm{,}7\text{<span style="font-weight: normal;font-style: normal;">mm</span>}\mathrm{,}}\end{array}$ ami majdnem egy nagyságrenddel kisebb a golyó $R=30$ mm-es sugaránál. Előzetes feltevésünk, mely szerint $\xi$ sokkal kisebb $R$-nél, utólag beigazolódott. A $T_{\infty }$ egyensúlyi hőmérsékletet becsüljük úgy, hogy a $\xi$ vastagságú kéreg hőmérséklete $T_2=0{}^{\circ }$C, azon belül pedig $T_1=100{}^{\circ }$C. A hőmérséklet kiegyenlítődését kifejező egyenlet: 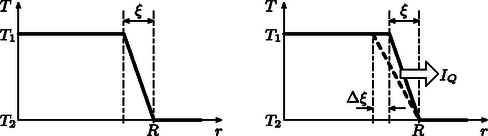$\begin{array}{c}{\displaystyle \frac{4}{3}\pi {\left(R-\xi \right)}^3{T}_1+\frac{4}{3}\pi \left[R^3-{\left(R-\xi \right)}^3\right]T_2=\frac{4}{3}\pi R^3{T}_{\infty }\mathrm{,}}\end{array}$ amiből $\xi \ll R$ felhasználásával (csak a $\xi$-ben elsőfokú tagokat tartva meg) megkapjuk a golyó egyensúlyi hőmérsékletét: $\begin{array}{c}{\displaystyle T_{\infty }\approx T_1-\frac{3\xi }{R}\left(T_1-T_2\right)\approx 63{}^{\circ }\text{<span style="font-weight: normal;font-style: normal;">C</span>}\mathrm{.}}\end{array}$ Mivel becslésről van szó, ezért az eredmény második értékes jegyét nem szabad nagyon komolyan vennünk.   II. megoldás. Használjuk a Fourier-törvényt, és közelítsük a hőmérsékletprofilt a 6. ábra bal oldalán látható, szakaszonként lineáris függvénnyel! (Könnyen belátható, hogy egy ilyen hőmérsékletprofil később nem marad szakaszonként lineáris, de ez a becslésünk érvényességét nem befolyásolja majd.)   6. ábra   A várhatóan kis $\xi$ behatolási mélység miatt a problémát kezelhetjük egydimenziósként (azaz golyó helyett egy végtelen féltér esetét vizsgáljuk). Tegyük fel, hogy $t$ idő után a ,,lineáris hidegfront'' szélessége $\xi$. Ekkor a golyó belsejéből a jeges vízbe átmenő hőáram nagysága (teljesítmény): $\begin{array}{c}{\displaystyle I_Q=\lambda A\frac{T_1-T_2}{\xi }\mathrm{.}}\end{array}$ (4) Ez a kiáramló teljesítmény okozza $\Delta t$ idő alatt a hidegfront $\Delta \xi$ szélesedését (6. ábra jobb oldala): $\begin{array}{c}{\displaystyle I_Q\Delta t=c\varrho A\left[T_1\Delta \xi +\frac{T_1+T_2}{2}\xi \right]-c\varrho A\frac{T_1+T_2}{2}\left(\xi +\Delta \xi \right)\mathrm{,}}\end{array}$ ahol a behatolási mélységnek megfelelő rész energiáját a szélein mért hőmérsékletek átlagának segítségével fejeztük ki. Ebből rendezés után adódik: $\begin{array}{c}{\displaystyle I_Q=c\varrho A\frac{T_1-T_2}{2}\frac{\Delta \xi }{\Delta t}\mathrm{.}}\end{array}$ (5) A hőáramokra kapott ($4$) és ($5$) összefüggéseket egyenlővé téve kapjuk: $\begin{array}{c}{\displaystyle \xi \Delta \xi =\frac{2\lambda }{c\varrho }\Delta t\mathrm{.}}\end{array}$ Összegezzük fel ennek az egyenletnek mindkét oldalát! Ekkor a jobb oldalon a vízbe merítés $t$ ideje, a bal oldalon pedig ${\xi }^2/2$ jelenik meg (ezt beláthatjuk pl. egy összenyomott rugóban tárolt energia analógiájával vagy integrálással). Tehát a ,,lineáris hidegfront'' behatolási mélysége az idő függvényében: $\begin{array}{c}{\displaystyle \xi \left(t\right)=2\sqrt[]{\frac{\lambda }{c\varrho }t}\sim \sqrt[]{t}\mathrm{,}}\end{array}$ ami egy 2-es faktor erejéig egyezik a dimenzióanalízis eredményével. A hőmérséklet kiegyenlítődését kifejező egyenlet ($\xi \ll R$ közelítésben): $\begin{array}{c}{\displaystyle \frac{4}{3}\pi {\left(R-\xi \right)}^3{T}_1+4\pi R^2\xi \frac{T_1+T_2}{2}\approx \frac{4}{3}\pi R^3{T}_{\infty }\mathrm{,}}\end{array}$ ebből $\begin{array}{c}{\displaystyle T_{\infty }\approx T_1-\frac{3\xi }{2R}\left(T_1-T_2\right)\mathrm{.}}\end{array}$ Végül a szakaszosan lineáris hőmérsékletprofilra levezetett $\xi$ behatolási mélységet felhasználva kapjuk a becslés végső formuláját: $\begin{array}{c}{\displaystyle T_{\infty }=T_1-\frac{3}{R}\sqrt[]{\frac{\lambda t}{c\varrho }}\left(T_1-T_2\right)\mathrm{.}}\end{array}$ Az adatokat behelyettesítve $T_{\infty }\approx 63{}^{\circ }\text{<span style="font-weight: normal;font-style: normal;">C</span>}$ egyensúlyi hőmérséklet adódik, egyezésben a dimenzióanalízissel kapott értékkel.