| Feladat: | B.4902 | Korcsoport: 16-17 | Nehézségi fok: nehéz |
| Megoldó(k): | Döbröntei Dávid Bence , Molnár-Sáska Zoltán | ||
| Füzet: | 2018/március, 156 - 158. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Feladat, Síkgeometriai bizonyítások, Helyvektorok, Háromszögek hasonlósága | ||
| Hivatkozás(ok): | Feladatok: 2017/október: B.4902 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A feladatot az (ideális egyenessel kibővített) projektív síkon, a Desargues-tétel többszöri alkalmazásával fogjuk igazolni. Ehhez néhány definíciót, és magát Desargues tételét mondjuk ki először. Ezután térjünk rá a feladat bizonyítására. Tetszőleges esetén jelölje az és egyenesek metszéspontját (mivel a megadott szakaszok különböző hosszúságúak, ezért a pontok nem ideális pontok). Legyen továbbá az egymással párhuzamos , , , egyenesek közös (ideális) pontja . Tekintsük az és a (ahol , , tetszőleges különböző indexek) háromszögeket. Mivel a két háromszög a pontra nézve perspektív, így Desargues tétele alapján tengelyesen is perspektív, azaz az , , az , , illetve az , egyenespárok , metszéspontjai egy egyenesre esnek (lásd az ábrát). 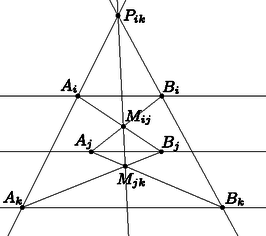 Az , , indexek megfelelő választásával adódik a következő hat darab ponthármasra, hogy az adott ponthármasok mind egy egyenesre esnek: (1) , , ; (2) , , ; (3) , , ; (4) , , ; (5) , , , illetve (6) , , mind (külön-külön) egy egyenesre esik. Továbbá mivel az és háromszögek a pontra nézve perspektívek, Desargues tétele alapján tengelyesen is perspektívek, azaz az , , az , , illetve az , egyenespárok , , metszéspontjai is (akár az imént) egy egyenesre esnek. Utoljára tekintsük az és háromszögeket. A fentiek szerint azaz a két háromszög a egyenesre perspektív, de akkor Desargues tétele alapján az és háromszögek pontra nézve is perspektívek, azaz az , és egyenesek valóban egy ponton mennek át. Döbröntei Dávid Bence (Pápa, Türr István Gimn. és Koll., 12. évf.) és Molnár-Sáska Zoltán (Budapesti Fazekas M. Gyak. Ált. Isk. és Gimn., 12. évf.) dolgozata alapján |